
分析 (1)方程整理后,利用平方根定义开方即可求出解;
(2)方程整理后,利用因式分解法求出解即可;
(3)方程利用配方法求出解即可.
解答 解:(1)方程整理得:(2x+3)2=25,
开方得:2x+3=5或2x+3=-5,
解得:x1=1,x2=-4;
(2)方程整理得:3x(x-2)-(x-2)=0,
分解因式得:(x-2)(3x-1)=0,
解得:x1=2,x2=$\frac{1}{3}$;
(3)方程整理得:x2-2x=2,
配方得:x2-2x+1=3,即(x-1)2=3,
开方得:x-1=±$\sqrt{3}$,
解得:x1=1+$\sqrt{3}$,x2=1-$\sqrt{3}$.
点评 此题考查了解一元二次方程-因式分解法,配方法,以及直接开平方法,熟练掌握各种解法是解本题的关键.


 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:填空题
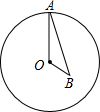 如图,点A为⊙O上一个动点,点B在⊙O内,且OA=2$\sqrt{3}$,OB=2,当∠OAB的度数取最大值时,AB的长度为2$\sqrt{2}$.
如图,点A为⊙O上一个动点,点B在⊙O内,且OA=2$\sqrt{3}$,OB=2,当∠OAB的度数取最大值时,AB的长度为2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
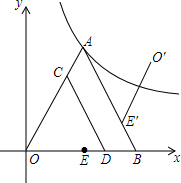 如图,在平面直角坐标系中,等边△OAB的顶点A落在反比例函数y=$\frac{9\sqrt{3}}{x}$上,OB在x轴正半轴上,中点为E,C为边OA上一点,过点C作CD∥AB交OB于D,以CD所在直线为对称轴将线段OE作轴对称变换得O′E′,设OC的长为x.
如图,在平面直角坐标系中,等边△OAB的顶点A落在反比例函数y=$\frac{9\sqrt{3}}{x}$上,OB在x轴正半轴上,中点为E,C为边OA上一点,过点C作CD∥AB交OB于D,以CD所在直线为对称轴将线段OE作轴对称变换得O′E′,设OC的长为x.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AO=CO,BO=DO,AB=BC | B. | AO=CO,BO=DO,AB=DC | ||
| C. | AB∥CD,AD∥BC,AO=CO | D. | AO=BO=CO=DO |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
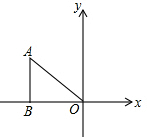 如图,Rt△ABO中,直角边BO落在x轴的负半轴上,点A的坐标是(-4,2),以O为位似中心,按比例尺1:2把△ABO缩小,则点A的对应点A′的坐标为( )
如图,Rt△ABO中,直角边BO落在x轴的负半轴上,点A的坐标是(-4,2),以O为位似中心,按比例尺1:2把△ABO缩小,则点A的对应点A′的坐标为( )| A. | (-1,2) | B. | (2,-1) | C. | (-2,1) | D. | (-2,1)或(2,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com