
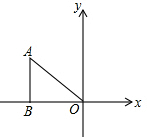
 如图,Rt△ABO中,直角边BO落在x轴的负半轴上,点A的坐标是(-4,2),以O为位似中心,按比例尺1:2把△ABO缩小,则点A的对应点A′的坐标为( )
如图,Rt△ABO中,直角边BO落在x轴的负半轴上,点A的坐标是(-4,2),以O为位似中心,按比例尺1:2把△ABO缩小,则点A的对应点A′的坐标为( )| A. | (-1,2) | B. | (2,-1) | C. | (-2,1) | D. | (-2,1)或(2,-1) |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
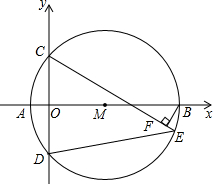 已知关于x的方程x2+(2m-6)x+m2-7=0有两个不相等的实数根,两根的平方和为10,且两根分别是A点和B点的横坐标(如图),以AB为直径作圆M交y轴于点C和点D,点E是$\widehat{BD}$上一点,BF⊥CE于点F,连接DE.
已知关于x的方程x2+(2m-6)x+m2-7=0有两个不相等的实数根,两根的平方和为10,且两根分别是A点和B点的横坐标(如图),以AB为直径作圆M交y轴于点C和点D,点E是$\widehat{BD}$上一点,BF⊥CE于点F,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2=(m-1)2,b2=4m2,c2=(m+1)2 | B. | a2=(m-1)2,b2=4m,c2=(m+1)2 | ||
| C. | a2=(m-1)2,b2=2m,c2=(m+1)2 | D. | a2=(m-1)2,b2=2m2,c2=(m+1)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
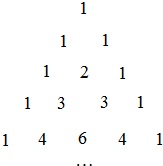 如图为杨辉三角表,它可以帮助我们按某种规律写出(a+b)n(n为自然数)展开式的系数,如:
如图为杨辉三角表,它可以帮助我们按某种规律写出(a+b)n(n为自然数)展开式的系数,如:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com