
【题目】如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB边上且DE⊥BE.
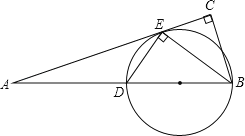
(1)判断直线AC与△DBE外接圆的位置关系,并说明理由;
(2)若AD=6,AE=6![]() ,求△DBE外接圆的半径及CE的长.
,求△DBE外接圆的半径及CE的长.
【答案】(1)直线AC与△DBE外接圆相切,理由见解析;(2)外接圆的半径为3,CE的长为2![]()
【解析】
(1)连接![]() ,根据直线与圆相切的判定定理,需证明
,根据直线与圆相切的判定定理,需证明![]() ,即
,即![]() ,已知
,已知![]() ,则需证明
,则需证明![]() ,根据等腰三角形
,根据等腰三角形![]() 结合
结合![]() 平分
平分![]() 的条件即可证明.
的条件即可证明.
(2)根据已知条件,可设圆的半径为![]() ,在
,在![]() 中根据勾股定理列方程解答即可;求
中根据勾股定理列方程解答即可;求![]() ,可过
,可过![]() 作
作![]() 于
于![]() ,根据角平分线的性质可得
,根据角平分线的性质可得![]() ,故在
,故在![]() 中用等面积法求
中用等面积法求![]() 即可.
即可.
解:(1)直线AC与△DBE外接圆相切.理由:
∵DE⊥BE
∴BD为△DBE外接圆的直径
取BD的中点O(即△DBE外接圆的圆心),连接OE
∴OE=OB
∴∠OEB=∠OBE
∵BE平分∠ABC
∴∠OBE=∠CBE
∴∠OEB=∠CBE
∵∠CBE+∠CEB=90°
∴∠OEB+∠CEB=90°
即OE⊥AC
∴直线AC与△DBE外接圆相切;
(2)设⊙O的半径为r,则在Rt△AOE中,AD=6,AO=r+6,AE=6![]() ,
,
OA2=OE2+AE2,
即:(r+6)2=r2+(6![]() )2,
)2,
解得:r=3
则△BDE的外接圆的半径为3.
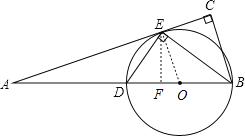
过点E作EF⊥AB于F,
∵BE平分∠ABC,∠C=90°
∴EF=EC
在Rt△AOE中,AO=6+3=9,
![]()
EF=![]()
∴CE=EF=2![]()
∴外接圆的半径为3,CE的长为2![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知⊙C的半径为2,圆外一点O满足OC=3.5,点P为⊙C上一动点,经过点O的直线l上有两点A、B,且OA=OB,∠APB=90°,l不经过点C,则AB的最小值为( )
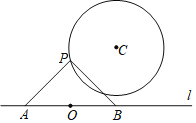
A. 2 B. 2.5 C. 3 D. 3.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设![]() 是
是![]() 的平均数,即
的平均数,即![]() ,则方差
,则方差![]() ,它反映了这组数的波动性,
,它反映了这组数的波动性,
(1)证明:对任意实数a,x1a,x2a,…,xna,与x1,x2,…,xn 方差相同;
(2)证明![]() ;
;
(3)以下是我校初三(1)班 10 位同学的身高(单位:厘米):
169,172,163,173,175,168,170,167,170,171,计算这组数的方差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,四边形ABCD为⊙O的内接四边形,点P在BA的延长线上,PD与⊙O相切,D为切点,若∠BCD=125°,则∠ADP的大小为( )
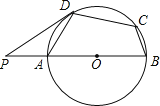
A.25°B.40°C.35°D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系内,已知A(2,3),B(4,1),直线l过P(m,0),A、B关于l的对称点分别为A’、B’,请利用直尺(无刻度)和圆规按下列要求作图.
(1)当A’与B重合时,请在图1中画出点P位置,并求出m的值;
(2)当A’、B’都落在y轴上时,请在图2中画出直线l,并求出m的值.
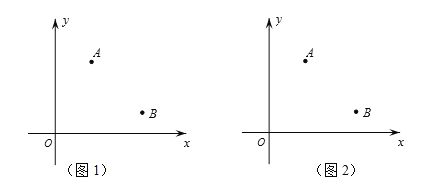
查看答案和解析>>
科目:初中数学 来源: 题型:
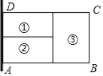
【题目】为了节省材料,某农场主利用围墙(围墙足够长)为一边,用总长为80m的篱笆围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等,则能围成的矩形区域ABCD的面积最大值是___m2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京第一条地铁线路于1971年1月15日正式开通运营.截至2017年1月,北京地铁共有19条运营线路,覆盖北京市11个辖区.据统计,2017 年地铁每小时客运量是2002年地铁每小时客运量的4倍,2017年客运240万人所用的时间比2002年客运240万人所用的时间少30小时,求2017年地铁每小时的客运量?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了方便游客观赏景点,某景区设计建造了如图所示的高为6米的观景台![]() ,且坡面
,且坡面![]() 的坡度比为1:1.后来为了方便行人推车(如子女带老人旅游等),决定降低坡度,新坡面的坡度比为
的坡度比为1:1.后来为了方便行人推车(如子女带老人旅游等),决定降低坡度,新坡面的坡度比为![]() .
.
(1)求新坡面的坡角![]() .
.
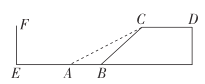
(2)原坡面底部的正前方13米(![]() 的长)有一座古建筑
的长)有一座古建筑![]() ,为保护文物,当地文物管理部门规定,坡面底部至少距古建筑7米,请问新的设计方案能否通过,试说明理由.(参考数据:
,为保护文物,当地文物管理部门规定,坡面底部至少距古建筑7米,请问新的设计方案能否通过,试说明理由.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com