
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЃЈaЃЌ0ЃЉЕуBЃЈbЃЌ0ЃЉЮЊxжсЩЯСНЕуЃЌЕуCдкYжсЕФе§АыжсЩЯЃЌЧвaЃЌbТњзуЕШЪНa2+2ab+b2=0ЃЎ
ЃЈ1ЃЉХаЖЯЁїABCЕФаЮзДВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌMЃЌNЪЧOCЩЯЕФЕуЃЌЧвЁЯCAM=ЁЯMAN=ЁЯNABЃЌбгГЄBNНЛACгкPЃЌСЌНгPMЃЌХаЖЯPMгыANЕФЮЛжУЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЎ
ЃЈ3ЃЉШчЭМ3ЃЌШєЕуDЮЊЯпЖЮBCЩЯЕФЖЏЕуЃЈВЛгыBЃЌCжиКЯЃЉЃЌЙ§ЕуDзїDEЁЭABгкEЃЌЕуGЮЊЯпЖЮDEЩЯвЛЕуЃЌЧвЁЯBGE=ЁЯACBЃЌFЮЊADЕФжаЕуЃЌСЌНгCFЃЌFGЃЎЧѓжЄЃКCFЁЭFGЃЎ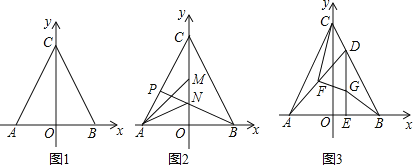
ЁОД№АИЁПЃЈ1ЃЉЁїABCЪЧЕШбќШ§НЧаЮЃЛЃЈ2ЃЉPMЁЮANЃЌжЄУїМћНтЮіЃЛЃЈ3ЃЉМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬтвтПЩЕУa=-bЃЌМДOA=OBЃЌИљОнЯпЖЮДЙжБЦНЗжЯпЕФаджЪПЩЕУAC=BCЃЌМДЁїABCЪЧЕШбќШ§НЧаЮЃЛ
ЃЈ2ЃЉбгГЄANНЛBCгкЕуEЃЌСЌНгPMЃЌЙ§ЕуMзїMHЁЭAEЃЌMDЁЭBPЃЌMGЁЭACЃЌИљОнЕШбќШ§НЧаЮЕФаджЪПЩЕУЁЯNAB=ЁЯNBAЃЌЁЯANO=ЁЯBNOЃЌПЩЕУЁЯPNC=ЁЯCNEЃЌИљОнНЧЦНЗжЯпЕФаджЪПЩЕУPMЦНЗжЁЯCPBЃЌИљОнШ§НЧаЮЕФЭтНЧЕФаджЪПЩЕУЁЯCPM=ЁЯCAN=2ЁЯNABЃЌМДПЩЕУPMЁЮANЃЛ
ЃЈ3ЃЉбгГЄGFжСЕуMЃЌЪЙFM=FGЃЌСЌНгCGЃЌCMЃЌAMЃЌгЩЬтвтПЩжЄЁїAMFЁеЁїDGFЃЌПЩЕУAM=DGЃЌгЩНЧЕФЪ§СПЙиЯЕПЩЕУЁЯBCO=ЁЯBDG=ЁЯDBGЃЌМДDG=BGЃЌИљОнЁАSASЁБПЩжЄЁїAMCЁеЁїBGCЃЌПЩЕУCM=CGЃЌИљОнЕШбќШ§НЧаЮаджЪПЩЕУCFЁЭFGЃЎ
НтЃКЃЈ1ЃЉЁпa2+2ab+b2=0ЃЌ
ЁрЃЈa+bЃЉ2=0ЃЌ
Ёрa=-bЃЌ
ЁрOA=OBЃЌЧвABЁЭOCЃЌ
ЁрOCЪЧABЕФДЙжБЦНЗжЯпЃЌ
ЁрAC=BCЃЌ
ЁрЁїACBЪЧЕШбќШ§НЧаЮ


 ПЊаФЭмзДдЊВтЪдОэЯЕСаД№АИ
ПЊаФЭмзДдЊВтЪдОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
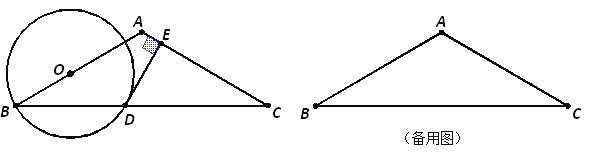
ЁОЬтФПЁПЖЈвхЃКШчЙћСНЬѕЯпЖЮНЋвЛИіШ§НЧаЮЗжГЩ3ИіаЁЕШбќШ§НЧаЮЃЌЮвУЧАбетСНЬѕЯпЖЮНазіетИіШ§НЧаЮЕФШ§ЗжЯпЃЎ
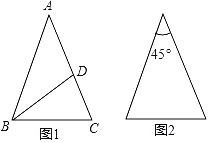
ЃЈ1ЃЉШчЭМ1ЃЌдкЁїABCжаЃЌABЃНACЃЌЕуDдкACБпЩЯЃЌЧвADЃНBDЃНBCЃЌЧѓЁЯAЕФДѓаЁЃЛ
ЃЈ2ЃЉдкЭМ1жаЙ§ЕуCзївЛЬѕЯпЖЮCEЃЌЪЙBDЃЌCEЪЧЁїABCЕФШ§ЗжЯпЃЛдкЭМ2жаЛГіЖЅНЧЮЊ45ЁуЕФЕШбќШ§НЧаЮЕФШ§ЗжЯпЃЌВЂБъзЂУПИіЕШбќШ§НЧаЮЖЅНЧЕФЖШЪ§ЃЛ
ЃЈ3ЃЉдкЁїABCжаЃЌЁЯBЃН30ЁуЃЌADКЭDEЪЧЁїABCЕФШ§ЗжЯпЃЌЕуDдкBCБпЩЯЃЌЕуEдкACБпЩЯЃЌЧвADЃНBDЃЌDEЃНCEЃЌЧыжБНгаДГіЁЯCЫљгаПЩФмЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
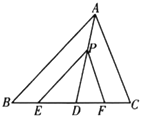
ЁОЬтФПЁПЧыдкЯТСаКсЯпЩЯзЂУїРэгЩЃЎ
ШчЭМЃЌдк![]() жаЃЌЕу
жаЃЌЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() дкБп
дкБп![]() ЩЯЃЌЕу
ЩЯЃЌЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЃЌШє
ЩЯЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЕН
ЕН![]() КЭ
КЭ![]() ЕФОрРыЯрЕШ.ЧѓжЄЃКЕу
ЕФОрРыЯрЕШ.ЧѓжЄЃКЕу![]() ЕН
ЕН![]() КЭ
КЭ![]() ЕФОрРыЯрЕШЃЎ
ЕФОрРыЯрЕШЃЎ
жЄУїЃКЁп![]() ЃЈвбжЊЃЉЃЌ
ЃЈвбжЊЃЉЃЌ
Ёр![]() ЃЈ______ЃЉЃЌ
ЃЈ______ЃЉЃЌ
Ёр![]() ЃЈ______ЃЉЃЌ
ЃЈ______ЃЉЃЌ
Ёп![]() ЃЈвбжЊЃЉЃЌ
ЃЈвбжЊЃЉЃЌ
Ёр![]() ЃЈ______ЃЉЃЌ
ЃЈ______ЃЉЃЌ
ЁпЕу![]() ЕН
ЕН![]() КЭ
КЭ![]() ЕФОрРыЯрЕШЃЈвбжЊЃЉЃЌ
ЕФОрРыЯрЕШЃЈвбжЊЃЉЃЌ
Ёр![]() ЪЧ
ЪЧ![]() ЕФНЧЦНЗжЯпЃЈ______ЃЉЃЌ
ЕФНЧЦНЗжЯпЃЈ______ЃЉЃЌ
Ёр![]() ЃЈНЧЦНЗжЯпЕФЖЈвхЃЉЃЌ
ЃЈНЧЦНЗжЯпЕФЖЈвхЃЉЃЌ
Ёр![]() ЃЈ______ЃЉЃЌ
ЃЈ______ЃЉЃЌ
МД![]() ЦНЗж
ЦНЗж![]() ЃЈНЧЦНЗжЯпЕФЖЈвхЃЉЃЌ
ЃЈНЧЦНЗжЯпЕФЖЈвхЃЉЃЌ
ЁрЕу![]() ЕН
ЕН![]() КЭ
КЭ![]() ЕФОрРыЯрЕШЃЈ______ЃЉЃЎ
ЕФОрРыЯрЕШЃЈ______ЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЕуAЃЈЈD3ЃЌ6ЃЉЁЂBЃЈЈD9ЃЌвЛ3ЃЉЃЌвддЕуOЮЊЮЛЫЦжааФЃЌЯрЫЦБШЮЊ![]() ЃЌАбЁїABOЫѕаЁЃЌдђЕуAЕФЖдгІЕуAЁфЕФзјБъЪЧЃЈ ЃЉ
ЃЌАбЁїABOЫѕаЁЃЌдђЕуAЕФЖдгІЕуAЁфЕФзјБъЪЧЃЈ ЃЉ

AЃЎЃЈЈD1ЃЌ2ЃЉ
BЃЎЃЈЈD9ЃЌ18ЃЉ
CЃЎЃЈЈD9ЃЌ18ЃЉЛђЃЈ9ЃЌЈD18ЃЉ
DЃЎЃЈЈD1ЃЌ2ЃЉЛђЃЈ1ЃЌЈD2ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
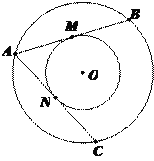
ЁОЬтФПЁПШчЭМЃЌДѓдВЕФЯвABЁЂACЗжБ№ЧааЁдВгкЕуMЁЂNЃЎ
ЃЈ1ЃЉЧѓжЄЃКAB=ACЃЛ
ЃЈ2ЃЉШєABЃН8ЃЌЧѓдВЛЗЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=AC=10ЃЌЁЯB=30ЁуЃЌOЪЧЯпЖЮABЩЯЕФвЛИіЖЏЕуЃЌвдOЮЊдВаФЃЌOBЮЊАыОЖзїЁбOНЛBCгкЕуDЃЌЙ§ЕуDзїжБЯпACЕФДЙЯпЃЌДЙзуЮЊEЃЎ
ЃЈ1ЃЉЧѓжЄЃКDEЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉЩшOB=xЃЌЧѓЁЯODEЕФФкВПгыЁїABCжиКЯВПЗжЕФУцЛ§yЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊвЛЬѕжБЯпЙ§Еу(0ЃЌ4)ЃЌЧвгыХзЮяЯпyЃН![]() x2НЛгкAЃЌBСНЕуЃЌЦфжаЕуAЕФКсзјБъЪЧЃ2.
x2НЛгкAЃЌBСНЕуЃЌЦфжаЕуAЕФКсзјБъЪЧЃ2.
(1)ЧѓетЬѕжБЯпЕФНтЮіЪНМАЕуBЕФзјБъЃЛ
(2)дкxжсЩЯЪЧЗёДцдкЕуCЃЌЪЙЕУЁїABCЪЧжБНЧШ§НЧаЮЃПШєДцдкЃЌЧѓГіЕуCЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
(3)Й§ЯпЖЮABЩЯвЛЕуPЃЌзїPMЁЮxжсЃЌНЛХзЮяЯпгкЕуMЃЌЕуMдкЕквЛЯѓЯоЃЌЕуN(0ЃЌ1)ЃЌЕБЕуMЕФКсзјБъЮЊКЮжЕЪБЃЌMNЃЋ3MPЕФГЄЖШзюДѓЃПзюДѓжЕЪЧЖрЩйЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬЕъОЯњвЛжжНЁЩэЧђЃЌвбжЊетжжНЁЩэЧђЕФГЩБОМлЮЊУПИі20дЊЃЌЪаГЁЕїВщЗЂЯжЃЌИУжжНЁЩэЧђУПЬьЕФЯњЪлСПyЃЈИіЃЉгыЯњЪлЕЅМлxЃЈдЊЃЉгаШчЯТЙиЯЕЃКy=Љ20x+80ЃЈ20ЁмxЁм40ЃЉЃЌЩшетжжНЁЩэЧђУПЬьЕФЯњЪлРћШѓЮЊwдЊЃЎ
ЃЈ1ЃЉЧѓwгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉИУжжНЁЩэЧђЯњЪлЕЅМлЖЈЮЊЖрЩйдЊЪБЃЌУПЬьЕФЯњЪлРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйдЊЃП
ЃЈ3ЃЉШчЙћЮяМлВПУХЙцЖЈетжжНЁЩэЧђЕФЯњЪлЕЅМлВЛИпгк28дЊЃЌИУЩЬЕъЯњЪлетжжНЁЩэЧђУПЬьвЊЛёЕУ150дЊЕФЯњЪлРћШѓЃЌЯњЪлЕЅМлгІЖЈЮЊЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯBAC=90ЁуЃЌAB=AC=2ЃЌвдABЮЊжБОЖЕФдВНЛBCгкDЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЮЊЃЈЁЁЁЁЃЉ

A. 1 B. 2 C. 1+![]() D. 2Љ
D. 2Љ![]()
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com