
【题目】请在下列横线上注明理由.
如图,在![]() 中,点
中,点![]() ,
,![]() ,
,![]() 在边
在边![]() 上,点
上,点![]() 在线段
在线段![]() 上,若
上,若![]() ,
,![]() ,点
,点![]() 到
到![]() 和
和![]() 的距离相等.求证:点
的距离相等.求证:点![]() 到
到![]() 和
和![]() 的距离相等.
的距离相等.
证明:∵![]() (已知),
(已知),
∴![]() (______),
(______),
∴![]() (______),
(______),
∵![]() (已知),
(已知),
∴![]() (______),
(______),
∵点![]() 到
到![]() 和
和![]() 的距离相等(已知),
的距离相等(已知),
∴![]() 是
是![]() 的角平分线(______),
的角平分线(______),
∴![]() (角平分线的定义),
(角平分线的定义),
∴![]() (______),
(______),
即![]() 平分
平分![]() (角平分线的定义),
(角平分线的定义),
∴点![]() 到
到![]() 和
和![]() 的距离相等(______).
的距离相等(______).
【答案】同位角相等,两直线平行;两直线平行,同位角相等;两直线平行,同位角相等;角的内部到角的两边距离相等的点在角的平分线上;等量代换;角平分线上的点到角的两边的距离相等.
【解析】
根据角平分线的性质及平行线的性质与判定即可解答.
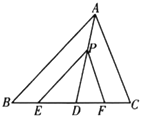
证明:∵∠PFD=∠C(已知),
∴PF∥AC(同位角相等,两直线平行),
∴∠DPF=∠DAC(两直线平行,同位角相等).
∵PE∥AB(已知),
∴ ∠EPD=∠BAD(两直线平行,同位角相等).
∵点 D到PE和PF的距离相等(已知),
∴ PD是 ∠EPF的角平分线(角的内部到角的两边距离相等的点在角的平分线上),
∴ ∠EPD=∠FPD(角平分线的定义),
∴∠BAD=∠DAC (等量代换),
即AD平分∠BAC (角平分线的定义),
∴点D到AB和AC的距离相等(角平分线上的点到角的两边的距离相等)


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
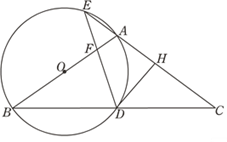
【题目】如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是圆O的切线;
(2)若![]() ,求证:A为EH的中点.
,求证:A为EH的中点.
(3)若EA=EF=1,求圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
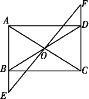
【题目】如图所示,在矩形ABCD中,O是AC与BD的交点,过点O的直线EF与AB,CD的延长线分别交于点E,F.
(1)求证:△BOE≌△DOF;
(2)当EF与AC满足什么条件时,四边形AECF是菱形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展课外球类特色的体育活动,决定开设A:羽毛球、B:篮球、C:乒乓球、 D:足球四种球类项目.为了解学生最喜欢哪一种活动项目(每人只选取一种),随机抽取了部分学生进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题.
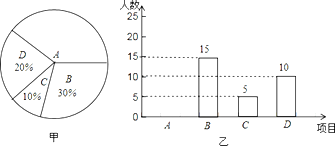
(1)样本中最喜欢A项目的人数所占的百分比为 ,其所在扇形统计图中对应的圆心角度数是 度;
(2)请把条形统计图补充完整;
(3)若该校有学生3000人,请根据样本估计全校最喜欢足球的学生人数约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了处理污水需要铺设一条长为2000米的管道,实际施工时,×××××××,设原计划每天铺设管道![]() 米,则可列方程
米,则可列方程![]() ,根据此情景,题目中的“×××××××”表示所丢失的条件,这一条件为( )
,根据此情景,题目中的“×××××××”表示所丢失的条件,这一条件为( )
A.每天比原计划多铺设10米,结果延期10天完成任务
B.每天比原计划少铺设10米,结果延期10天完成任务
C.每天比原计划少铺设10米,结果提前10天完成任务
D.每天比原计划多铺设10米,结果提前10天完成任务
查看答案和解析>>
科目:初中数学 来源: 题型:
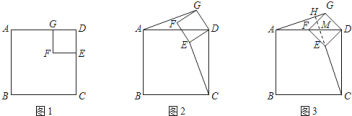
【题目】如图![]() ,若四边形
,若四边形![]() 、四边形
、四边形![]() 都是正方形,显然图中有
都是正方形,显然图中有![]() ,
,![]() ;
;
![]() 当正方形
当正方形![]() 绕
绕![]() 旋转到如图
旋转到如图![]() 的位置时,
的位置时,![]() 是否成立?若成立,请给出证明;若不成立,请说明理由;
是否成立?若成立,请给出证明;若不成立,请说明理由;
![]() 当正方形
当正方形![]() 绕
绕![]() 旋转到如图
旋转到如图![]() 的位置时,延长
的位置时,延长![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() .
.
①求证:![]() ;
;
②当![]() ,
,![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的方程:mx2﹣(3m﹣1)x+2m﹣2=0.
(1)求证:无论m取何值时,方程恒有实数根;
(2)若关于x的二次函数y=mx2﹣(3m﹣1)x+2m﹣2的图象与x轴两交点间的距离为2时,求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点A(a,0)点B(b,0)为x轴上两点,点C在Y轴的正半轴上,且a,b满足等式a2+2ab+b2=0.
(1)判断△ABC的形状并说明理由;
(2)如图2,M,N是OC上的点,且∠CAM=∠MAN=∠NAB,延长BN交AC于P,连接PM,判断PM与AN的位置关系,并证明你的结论.
(3)如图3,若点D为线段BC上的动点(不与B,C重合),过点D作DE⊥AB于E,点G为线段DE上一点,且∠BGE=∠ACB,F为AD的中点,连接CF,FG.求证:CF⊥FG.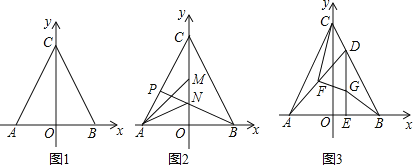
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点,且∠EAF=60°,请探究图中线段BE,EF,FD之间的数量关系是什么?
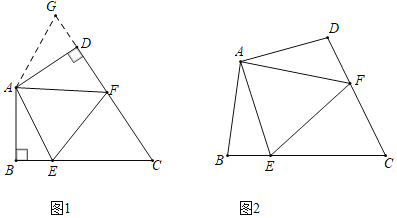
小明探究此问题的方法是:延长FD到点G,使DG=BE,连结AG.先证明△ABE≌△ADG,得AE=AG;再由条件可得∠EAF=∠GAF,证明△AEF≌△AGF,进而可得线段BE,EF,FD之间的数量关系是 .
(2)拓展应用:
如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=![]() ∠BAD.问(1)中的线段BE,EF,FD之间的数量关系是否还成立?若成立,请给出证明;若不成立,请说明理由.
∠BAD.问(1)中的线段BE,EF,FD之间的数量关系是否还成立?若成立,请给出证明;若不成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com