
【题目】已知:如图,![]() 、
、![]() 都是等腰三角形,且
都是等腰三角形,且![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 相交于点
相交于点![]() ,点
,点![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 的中点.以下
的中点.以下![]() 个结论:①
个结论:①![]() ;②
;②![]() ;③
;③![]() 是等边三角形;④连
是等边三角形;④连![]() ,则
,则![]() 平分
平分![]() .正确的是( )
.正确的是( )
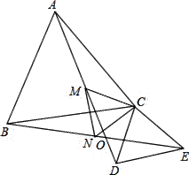
A.①②③B.①②④C.①③④D.①②③④
【答案】B
【解析】
①根据∠ACB=∠DCE求出∠ACD=∠BCE,证出![]() 即可得出结论,故可判断;
即可得出结论,故可判断;
②根据全等求出∠CAD=∠CBE,根据三角形外角定理得∠DOB=∠OBA+∠BAO,通过等角代换能够得到∠DOB=∠CBA+∠BAC,根据三角形内角和定理即可求出∠CBA+∠BAC,即可求出∠DOB,故可判断;
③根据已知条件可求出AM=BN,根据SAS可求出![]() ,推出CM=CN,∠ACM=∠BCN,然后可求出∠MCN=∠ACB=α,故可判断
,推出CM=CN,∠ACM=∠BCN,然后可求出∠MCN=∠ACB=α,故可判断![]() 的形状;
的形状;
④在AD上取一点P使得DP=EO,连接CP,根据![]() ,可求出∠CEO=∠CDP,根据SAS可求出
,可求出∠CEO=∠CDP,根据SAS可求出 ![]() ,可得∠COE=∠CPD,CP=CO,进而得到 ∠COP=∠COE,故可判断.
,可得∠COE=∠CPD,CP=CO,进而得到 ∠COP=∠COE,故可判断.
①正确,理由如下:
∵![]() ,
,
∴∠ACB+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE,
又∵CA=CB,CD=CE,
∴![]() (SAS),
(SAS),
∴AD=BE,
故①正确;
②正确,理由如下:
由①知,![]() ,
,
∴∠CAD=∠CBE,
∵∠DOB为![]() 的外角,
的外角,
∴∠DOB=∠OBA+∠BAO=∠EBC+∠CBA+∠BAO=∠DAC+∠BAO+∠CBA=∠CBA+∠BAC,
∵∠CBA+∠BAC+∠ACB=180°,∠ACB=α,
∴∠CBA+∠BAC=180°-α,
即∠DOB=180°-α,
故②正确;
③错误,理由如下:
∵点![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 的中点,
的中点,
∴AM= ![]() AD,BN=
AD,BN= ![]() BE,
BE,
又∵由①知,AD=BE,
∴AM=BN,
又∵∠CAD=∠CBE,CA=CB,
∴![]() (SAS),
(SAS),
∴CM=CN,∠ACM=∠BCN,
∴∠MCN=∠MCB+∠CBN=∠MCB+∠ACM=∠ACB=α,
∴![]() 为等腰三角形且∠MCN=α,
为等腰三角形且∠MCN=α,
∴![]() 不是等边三角形,
不是等边三角形,
故③错误;
④正确,理由如下:

如图所示,在AD上取一点P使得DP=EO,连接CP,
由①知,![]() ,
,
∴∠CEO=∠CDP,
又∵CE=CD,EO=DP,
∴![]() (SAS),
(SAS),
∴∠COE=∠CPD,CP=CO,
∴∠CPO=∠COP,
∴∠COP=∠COE,
即OC平分∠AOE,
故④正确;
故答案为:B.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】填空并完成以下证明:
已知:点P在直线CD上,∠BAP+∠APD=180°,∠1=∠2.
求证:AB∥CD,∠E=∠F.
证明:∵∠BAP+∠APD=180°,(已知)
∴AB∥ .( )
∴∠BAP= .( )
又∵∠1=∠2,(已知)
∠3= ﹣∠1,
∠4= ﹣∠2,
∴∠3= (等式的性质)
∴AE∥PF.( )
∴∠E=∠F.( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有甲、乙两个可以自由转动的转盘,其中转盘甲被平均分成三个扇形,转盘乙被平均分成五个扇形.小明与小亮玩转盘游戏,规则如下:同时转动两个转盘,转盘停止后,转盘甲指针所指数字作为点的横坐标,转盘乙指针所指数字作为点的纵坐标(当指针指在边界线时视为无效,重转),从而确定一个点的坐标为A(m,n).当点A在第一象限时,小明赢;当点A在第二象限时,小亮赢.请你利用画树状图或列表法分析该游戏规则对双方是否公平?并说明理由.
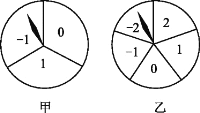
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示.有下列结论:①b2-4ac<0;②ab>0;③a-b+c=0;④4a+b=0;⑤当y=2时,x只能等于0.其中正确的是( )
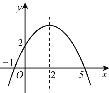
A. ①④ B. ③④ C. ②⑤ D. ③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一袋中装有形状大小都相同的四个小球,每个小球上各标有一个数字,分别是1,4,7,8.现规定从袋中任取一个小球,对应的数字作为一个两位数的个位数;然后将小球放回袋中并搅拌均匀,再任取一个小球,对应的数字作为这个两位数的十位数.
(1)写出按上述规定得到所有可能的两位数;
(2)从这些两位数中任取一个,求其算术平方根大于4且小于7的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
(1)求证:CD是⊙O的切线;
(2)若BC=3,CD=4,求平行四边形OABC的面积.
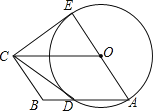
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你能求![]() 的值吗?遇到这样的问题,我们可以先思考一下,从简单的情形入手.先分别计算下列各式的值.
的值吗?遇到这样的问题,我们可以先思考一下,从简单的情形入手.先分别计算下列各式的值.
①![]()
②![]()
③![]() ……
……
(1)由此我们可以得到:![]()
请你利用上面的结论,再完成下面两题的计算:
(2)250+249+248+…+22+2+1
(3)若![]() ,求x2020的值
,求x2020的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列各组条件中,不能说明![]() 的是( )
的是( )
A.AB=DE,∠B=∠E,∠C=∠FB.AB=DE,∠A=∠D,∠B=∠E
C.AC=DF,BC=EF,∠A=∠DD.AB=DE,BC=EF,AC=ED
查看答案和解析>>
科目:初中数学 来源: 题型:
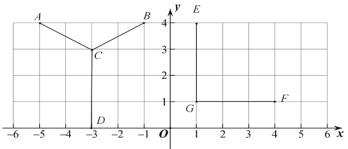
【题目】(1)写出点![]() 的坐标
的坐标
(2)线段![]() 先向____________平移____________个单位长度,再向____________平移____________单位长度,平移后的线段与线段
先向____________平移____________个单位长度,再向____________平移____________单位长度,平移后的线段与线段![]() 重合.
重合.
(3)已知在![]() 轴上存在点
轴上存在点![]() 与
与![]() 围成的三角形面积为6,请写出
围成的三角形面积为6,请写出![]() 的坐标
的坐标
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com