
分析 (1)根据题中给出的例子列式计算即可;
(2)分别求出a※b与b※a的值即可;
(3)先根据题意得出a,b的值,代入代数式进行计算即可.
解答 解:(1)∵1※3=1×4+3=7,3※(-1)=3×4-1=11,5※4=5×4+4=24,
∴4※3=4×4+3=19,a※b=4a+b.
故答案为:19,4a+b;
(2)∵a※b=4a+b,b※a=4b+a,
∴a※b≠b※a.
故答案为:≠;
(3)∵(a-$\frac{1}{2}$)2※|b+$\frac{1}{3}$|=4(a-$\frac{1}{2}$)2+|b+$\frac{1}{3}$|=0,
∴a=$\frac{1}{2}$,b=-$\frac{1}{3}$,
∴[(a2-ab)※(2a2+3ab)]※(-20a2+5ab)
=[($\frac{1}{4}$+$\frac{1}{6}$)※($\frac{1}{2}$-$\frac{1}{2}$)]※(-5-$\frac{5}{6}$)
=[$\frac{5}{12}$※0]※(-$\frac{35}{6}$)
=(4×$\frac{5}{12}$)※(-$\frac{35}{6}$)
=$\frac{5}{3}$※(-$\frac{35}{6}$)
=4×$\frac{5}{3}$-$\frac{35}{6}$
=$\frac{20}{3}$-$\frac{35}{6}$
=$\frac{5}{6}$.
点评 本题考查的是有理数的混合运算,熟知有理数混合运算的法则是解答此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 小明从如图中的二次函数y=ax2+bx+c图象中,观察得出了下面的五条信息:①b<0;②c=0;③函数的最小值为-3;④4a+2b-5c<0;⑤当x1<x2<2时,y1>y2.你认为其中正确的有①②③④⑤.
小明从如图中的二次函数y=ax2+bx+c图象中,观察得出了下面的五条信息:①b<0;②c=0;③函数的最小值为-3;④4a+2b-5c<0;⑤当x1<x2<2时,y1>y2.你认为其中正确的有①②③④⑤.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,某酒店大门的旋转门内部由三块宽为2米,高为3米的玻璃隔板组成,三块玻璃摆放时夹角相同.若入口处两根立柱之间的距离为2米,则两立柱底端中点到中央转轴底端的距离为( )
如图,某酒店大门的旋转门内部由三块宽为2米,高为3米的玻璃隔板组成,三块玻璃摆放时夹角相同.若入口处两根立柱之间的距离为2米,则两立柱底端中点到中央转轴底端的距离为( )| A. | $\sqrt{3}$米 | B. | 2米 | C. | 2$\sqrt{2}$米 | D. | 3米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
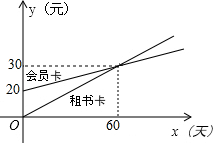 某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡,使用这两种卡租书,租书金额y(元)与租书时间x(天)之间的关系如图所示.
某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡,使用这两种卡租书,租书金额y(元)与租书时间x(天)之间的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a+49b}{100}$ | B. | $\frac{51a+b}{100}$ | C. | $\frac{a+b}{100}$ | D. | $\frac{51a+49b}{100}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com