
【题目】如图,一个长方形盒子的长、宽、高分别是4cm,4cm,6cm
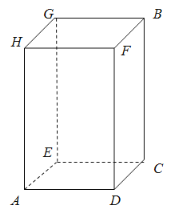
(1)一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点B,请你帮蚂蚁设计一条最短的路线,蚂蚁要爬行的最短路线是多少?
(2)若将一根木棒放进盒子里并能盖上盖子,则能放入改盒子里的木棒的最大长是多少cm?(结果可保留根号)
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知![]() ,
,![]() ,
,![]() .
.
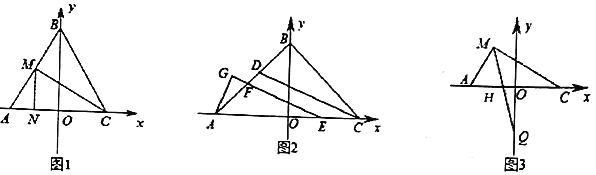
(1)如图1,若![]() ,
,![]() 于点
于点![]() ,
,![]() 轴交
轴交![]() 于点
于点![]() ,则
,则![]() _____.
_____.
(2)如图2,若![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() ,过
,过![]() 上一点作
上一点作![]() ,交
,交![]() 于点
于点![]() ,
,![]() 是
是![]() 的高,探究
的高,探究![]() 与
与![]() 的数量关系;
的数量关系;
(3)如图3,在(1)的条件下,![]() 上点
上点![]() 满足
满足![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 PQ 上有一点 O,点 A 为直线外一点,连接 OA,在直线 PQ 上找一点 B,使得△AOB 是等腰三角形,这样的点 B 有_____个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“分别以两条已知线段为腰和底边上的高作等腰三角形”的尺规作图过程.
已知:线段 a, b.
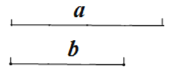
求作:等腰△ABC,使线段 a 为腰,线段 b 为底边 BC 上的高. 作法:如图,
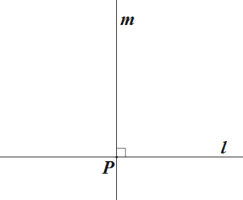
①画直线 l,作直线 m⊥l,垂足为 P;
②以点 P 为圆心,线段 b 的长为半径画弧,交直线 m 于点 A;
③以点 A 为圆心,线段 a 的长为半径画弧,交直线 l 于 B,C 两点;
④分别连接 AB, AC;
所以△ABC 就是所求作的等腰三角形. 根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵ = ,
∴△ABC 为等腰三角形( )(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)如图,已知抛物线y=x2+bx+c经过A(-1,0),B(3,0)两点.
(1)求抛物线的解析式和顶点坐标;
(2)当0<x<3时,求y的取值范围;
(3)点P为抛物线上一点,若S△PAB=10,求出此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,连结CE交AD于点F,连结BD交CE于点G,连结BE.下列结论:①CE=BD;②△ADC是等腰直角三角形;③∠ADB=∠AEB;④S四边形BCDE=![]() BD·CE;⑤BC2+DE2=BE2+CD2.其中正确的结论有( )
BD·CE;⑤BC2+DE2=BE2+CD2.其中正确的结论有( )
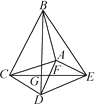
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从货场![]() 出发,向东走2千米到达批发部
出发,向东走2千米到达批发部![]() ,继续向东走1.5千米到达商场
,继续向东走1.5千米到达商场![]() ,又向西走5.5千米到达超市
,又向西走5.5千米到达超市![]() ,最后回到货场.
,最后回到货场.
(1)以货场为原点,以东为正方向,用一个单位长度表示1千米,你能在数轴上分别表示出货场![]() ,批发部
,批发部![]() ,商场
,商场![]() ,超市
,超市![]() 的位置吗?
的位置吗?
(2)超市![]() 距离货场
距离货场![]() 多远?
多远?
(3)此货车每千米耗油0.1升,每升汽油6.20元,请计算此货车一共需要多少汽油费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在抗洪抢险中,人民解放军的冲锋舟沿南北方向的河流抢救灾民.约定向北为正方向,某冲锋舟从 A 地出发,到达B地的一趟的航程记录如下(单位:千米):
![]()
(1)B地在A地的何方?相距多少千米?
(2)若冲锋舟每千米耗油![]() 升,油箱的容量为29 升,则途中至少需要补充多少升油?
升,油箱的容量为29 升,则途中至少需要补充多少升油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为12,点E在边AB上,BE=8,过点E作EF∥BC,分别交BD、CD于G、F两点.若点P、Q分别为DG、CE的中点,则PQ的长为_____.
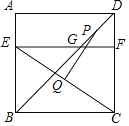
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com