Question

【题目】已知：如图①，在矩形ABCD中，AB=5，AD= ，AE⊥BD，垂足是E．点F是点E关于AB的对称点，连接AF，BF．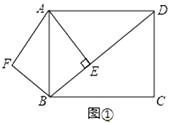

（1）求AE和BE的长；
（2）若将△ABF沿着射线BD方向平移，设平移的距离为m（平移距离指点B沿BD方向所经过的线段长度）．当点F分别平移到线段AB、AD上时，直接写出相应的m的值；
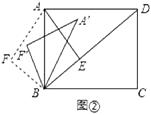
（3）如图②，将△ABF绕点B顺时针旋转一个角α（0°＜α＜180°），记旋转中的△ABF为△A′BF′，在旋转过程中，设A′F′所在的直线与直线AD交于点P．与直线BD交于点Q．是否存在这样的P、Q两点，使△DPQ为等腰三角形？若存在，求出此时DQ的长；若不存在，请说明理由．

Answer 1

【答案】
（1）

解：在Rt△ABD中，AB=5，AD= ，

由勾股定理得：BD= = = ．

∵S△ABD= BDAE= ABAD，

∴AE= = =4．

在Rt△ABE中，AB=5，AE=4，

由勾股定理得：BE=3

（2）

解：设平移中的三角形为△A′B′F′，如答图2所示：

由对称点性质可知，∠1=∠2．

由平移性质可知，AB∥A′B′，∠4=∠1，BF=B′F′=3．

①当点F′落在AB上时，

∵AB∥A′B′，

∴∠3=∠4，

∴∠3=∠2，

∴BB′=B′F′=3，即m=3；

②当点F′落在AD上时，

∵AB∥A′B′，

∴∠6=∠2，

∵∠1=∠2，∠5=∠1，

∴∠5=∠6，

又易知A′B′⊥AD，

∴△B′F′D为等腰三角形，

∴B′D=B′F′=3，

∴BB′=BD﹣B′D= ﹣3= ，即m=

（3）

解：存在．理由如下：

在旋转过程中，等腰△DPQ依次有以下4种情形：

①如答图3﹣1所示，点Q落在BD延长线上，且PD=DQ，易知∠2=2∠Q，

∵∠1=∠3+∠Q，∠1=∠2，

∴∠3=∠Q，

∴A′Q=A′B=5，

∴F′Q=F′A′+A′Q=4+5=9．

在Rt△BF′Q中，由勾股定理得：BQ= = =3 ．

∴DQ=BQ﹣BD=3 ﹣ ；

②如答图3﹣2所示，点Q落在BD上，且PQ=DQ，易知∠2=∠P，

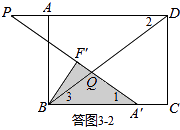
∵∠1=∠2，

∴∠1=∠P，

∴BA′∥PD，则此时点A′落在BC边上．

∵∠3=∠2，

∴∠3=∠1，

∴BQ=A′Q，

∴F′Q=F′A′﹣A′Q=4﹣BQ．

在Rt△BQF′中，由勾股定理得：BF′2+F′Q2=BQ2，

即：32+（4﹣BQ）2=BQ2，

解得：BQ= ，

∴DQ=BD﹣BQ= ﹣ = ；

③如答图3﹣3所示，点Q落在BD上，且PD=DQ，易知∠3=∠4．

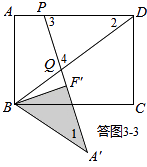
∵∠2+∠3+∠4=180°，∠3=∠4，

∴∠4=90°﹣ ∠2．

∵∠1=∠2，

∴∠4=90°﹣ ∠1．

∴∠A′QB=∠4=90°﹣ ∠1，

∴∠A′BQ=180°﹣∠A′QB﹣∠1=90°﹣ ∠1，

∴∠A′QB=∠A′BQ，

∴A′Q=A′B=5，

∴F′Q=A′Q﹣A′F′=5﹣4=1．

在Rt△BF′Q中，由勾股定理得：BQ= = = ，

∴DQ=BD﹣BQ= ﹣ ；

④如答图3﹣4所示，点Q落在BD上，且PQ=PD，易知∠2=∠3．

∵∠1=∠2，∠3=∠4，∠2=∠3，

∴∠1=∠4，

∴BQ=BA′=5，

∴DQ=BD﹣BQ= ﹣5= ．

综上所述，存在4组符合条件的点P、点Q，使△DPQ为等腰三角形；

DQ的长度分别为3 ﹣ 或 或 ﹣ 或

【解析】（1）利用矩形性质、勾股定理及三角形面积公式求解；（2）依题意画出图形，如答图2所示．利用平移性质，确定图形中的等腰三角形，分别求出m的值；（3）在旋转过程中，等腰△DPQ有4种情形，如答图3所示，对于各种情形分别进行计算．
【考点精析】本题主要考查了勾股定理的概念的相关知识点，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题．