
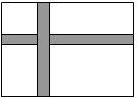
 要在长为32米,宽为20米的矩形花圃中修两条与花圃四周垂直等宽的小路(如图),且使种植花草的面积能达到589平方米,问小路应修多宽?
要在长为32米,宽为20米的矩形花圃中修两条与花圃四周垂直等宽的小路(如图),且使种植花草的面积能达到589平方米,问小路应修多宽? 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
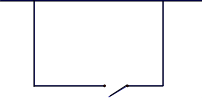 用38m长的竹篱笆建一个矩形养鸡场,养鸡场一面用砖砌成,其它用竹篱笆围成,并且在与砖墙相对的一面开2m的门(门不用篱笆),问怎样围竹篱笆,使得养鸡场占地面积最大?最大面积是多少?
用38m长的竹篱笆建一个矩形养鸡场,养鸡场一面用砖砌成,其它用竹篱笆围成,并且在与砖墙相对的一面开2m的门(门不用篱笆),问怎样围竹篱笆,使得养鸡场占地面积最大?最大面积是多少?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 35×10-9 | B. | 3.5×10-6 | C. | 3.5×10-9 | D. | 35×10-7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com