
【题目】如图,在菱形ABCD中,AB=BD,点E、F分别在AB,AD上,且AE=DF,连接BF与DE,相交于点G,连接CG,与BD相交于点H,下列结论①△AED≌△DFB;②S四边形BCDG=![]() CG2;③若AF=2FD,则BG=6GF,其中正确的有____________.(填序号)
CG2;③若AF=2FD,则BG=6GF,其中正确的有____________.(填序号)
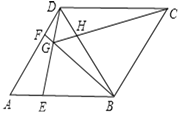
【答案】①②③
【解析】
对于①,先证明△ABD为等边三角形,再根据“SAS”证明△AED≌△DFB;
②,先证明∠BGE=60°=∠BCD,从而得点B、C、D、G四点共圆,因此∠BGC=∠DGC=60°,如图,过点C作CM⊥GB于M,CN⊥GD于N,再证明△CBM≌△CDN,所以S 四边形BCDG=S 四边形CMGN,求后者的面积即得答案;
③,过点F作FP∥AE于P点,根据平行线分线段成比例定理即可得出结论.
解:①∵ABCD为菱形,∴AB=AD.
∵AB=BD,∴AB=AD=BD,
∴△ABD为等边三角形.
∴∠A=∠BDF=60°.
又∵AE=DF,AD=BD,
∴△AED≌△DFB,故①正确;
②∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°=∠BCD,
即∠BGD+∠BCD=180°,
∴点B、C、D、G四点共圆,
∴∠BGC=∠BDC=60°,∠DGC=∠DBC=60°.
∴∠BGC=∠DGC=60°.
如图,过点C作CM⊥GB于M,CN⊥GD于N,则CM=CN.
∴Rt△CBM≌Rt△CDN(HL),
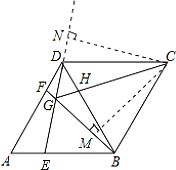
∴S 四边形BCDG=S 四边形CMGN,S 四边形CMGN=2S △CMG,
∵∠CGM=60°,
∴GM= ![]() CG,CM=
CG,CM= ![]() CG,
CG,
∴S 四边形CMGN=2S △CMG=2×![]() ×GM×CM=2×
×GM×CM=2×![]() ×
×![]() CG×
CG× ![]() CG=
CG= ![]() CG 2,故②正确;
CG 2,故②正确;
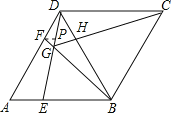
③如图,过点F作FP∥AE于P点.
∵AF=2FD,
∴FP:AE=DF:DA=1:3,
∵AE=DF,AB=AD,
∴BE=2AE,
∴FP:BE=1:6=FG:BG,
即BG=6GF,故③正确.
综上所述,正确的结论有①②③.
故答案为:①②③.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】为了推动阳光体育运动的广泛开展,引导学生走向操场,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了统计图①和图②,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为______,图①中![]() 的值为_____;
的值为_____;
(2)本次调查获取的样本数据的众数为______,中位数为________;
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?

查看答案和解析>>
科目:初中数学 来源: 题型:
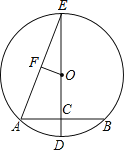
【题目】如图,在⊙O中,DE是⊙O的直径,AB是⊙O的弦,AB的中点C在直径DE上.已知AB=8cm,CD=2cm
(1)求⊙O的面积;
(2)连接AE,过圆心O向AE作垂线,垂足为F,求OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解方程。
(1)4(x-3) ![]() =36
=36
(2)x2-4x+1=0.
(3)![]() -7x+6=0
-7x+6=0
(4)![]()
(5)(y-1)2+2y(1-y)=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角△ABC中,∠C=90°,D为BC的中点,将△ABC折叠,使点A与点D重合,EF为折痕,则sin∠BED的值是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是一次函数y=2x的图象与反比例函数y=![]() 的图象在第一象限内的交点,AB⊥x轴于点B,点C在x轴的负半轴上,且∠ACB=∠OAB,△OAB的面积为4,则点C的坐标为( )
的图象在第一象限内的交点,AB⊥x轴于点B,点C在x轴的负半轴上,且∠ACB=∠OAB,△OAB的面积为4,则点C的坐标为( )

A.(﹣8,0)B.(﹣6,0)C.(﹣![]() ,0)D.(﹣
,0)D.(﹣![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
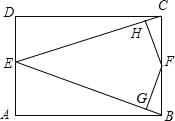
【题目】如图,在矩形ABCD中,AB=3,BC=2,点E为AD中点,点F为BC边上任一点,过点F分别作EB,EC的垂线,垂足分别为点G,H,则FG+FH为( ).
A.![]() B.
B.![]()
![]() C.
C.![]()
![]() D.
D.![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以点P(-1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=![]() ,将△ABC绕点P旋转180°,得到△MCB.
,将△ABC绕点P旋转180°,得到△MCB.

(1)求B、C两点的坐标;
(2)请在图中画出线段MB、MC,并判断四边形ACMB的形状(不必证明),求出点M的坐标;
(3)动直线l从与BM重合的位置开始绕点B顺时针旋转,到与BC重合时停止,设直线l与CM交点为E,点Q为BE的中点,过点E作EG⊥BC于G,连接MQ、QG.请问在旋转过程中∠MQG的大小是否变化?若不变,求出∠MQG的度数;若变化,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com