
(本题满分12分)已知直线y=kx+6(k<0)分别交x轴、y轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒2个单位长度,过点P作x轴的垂线交直线AB于点C,设运动时间为t秒.

(1)当k=-1时,线段OA上另有一动点Q由点A向点O运动,它与点P以相同速度同时出发,当点P到达点A时两点同时停止运动(如图1).
①直接写出t=1秒时C、Q两点的坐标;
②若以Q、C、A为顶点的三角形与△AOB相似,求t的值.
(2)当 时,设以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D(如图2),①求CD的长; ②设△COD的OC边上的高为h,当t为何值时,h的值最大?
时,设以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D(如图2),①求CD的长; ②设△COD的OC边上的高为h,当t为何值时,h的值最大?
见解析
【解析】
试题分析:(1)①当k=-1时,直线y=-x+6与x轴、y轴的交点A、B坐标分别是(6,0)(0,6),t=1
秒时,AQ=2,OP=2,所以可求C、Q两点的坐标;②分两种情况讨论:当△AQC∽△AOB时,可求t=1.5,当△ACQ∽△AOB时,可求t=2;(2)①根据题意得点C的坐标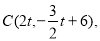 则以C为顶点的抛物线是
则以C为顶点的抛物线是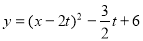 ,然后表示出抛物线与直线y=
,然后表示出抛物线与直线y=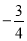 x+6的交点坐标,过点D作DE⊥CP于点E,利用△DEC∽△AOB,可得
x+6的交点坐标,过点D作DE⊥CP于点E,利用△DEC∽△AOB,可得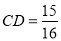 ; ②当
; ②当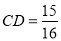 ,可求S△COD为定值
,可求S△COD为定值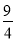 ,要使OC边上的高h的值最大,只要OC最短,当OC⊥AB时OC,最短,此时OC的长为
,要使OC边上的高h的值最大,只要OC最短,当OC⊥AB时OC,最短,此时OC的长为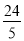 ,然后根据Rt△PCO∽Rt△OAB.可得
,然后根据Rt△PCO∽Rt△OAB.可得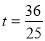 .
.
试题解析:【解析】
(1)①C(2,4),Q(4,0) 2分
②由题意得:P(2t,0),C(2t,-2t+6),Q(6-2t,0)
分两种情况讨论:
情形一:当△AQC∽△AOB时,∠AQC=∠AOB=90°,
∴CQ⊥OA.
∵CP⊥OA,∴点P与点Q重合,OQ=OP,即6-2t=2t,∴t=1.5
情形二:当△ACQ∽△AOB时,∠ACQ=∠AOB=90°,∵OA=OB=6,
∴△AOB是等腰直角三角形,∴△ACQ也是等腰直角三角形,
∵CP⊥OA,∴AQ=2CP,即2t=2(-2t+6),
∴t=2,∴满足条件的t的值是1.5秒或2秒. 6分
(2)①由题意得: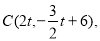
∴以C为顶点的抛物线解析式是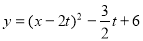 ,
,
由 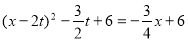 解得
解得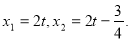
过点D作DE⊥CP于点E,
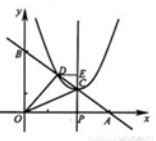
则∠DEC=∠AOB=90°.
∵DE∥OA,∴∠EDC=∠OAB,
∴△DEC∽△AOB,∴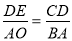 ,∵AO=8,AB=10,
,∵AO=8,AB=10,
DE=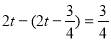 ,∴CD=
,∴CD= 9分
9分
②∵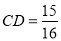 ,CD边上的高=
,CD边上的高=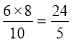 ,
, 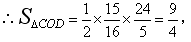
∴S△COD为定值.要使OC边上的高h的值最大,只要OC最短,当OC⊥AB时OC
最短,此时OC的长为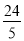 ,∠BCO=90°,
,∠BCO=90°,
∵∠AOB=90°∴∠COP=90°﹣∠BOC=∠OBA,
又∵CP⊥OA,∴Rt△PCO∽Rt△OAB.
∴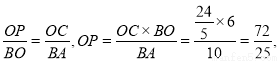 即
即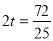 ,∴
,∴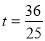
∴当t为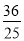 秒时,h的值最大. 12分
秒时,h的值最大. 12分
考点:1.一次函数;2.二次函数与一次函数的交点;3.相似三角形的判定与性质;4.分类讨论.


科目:初中数学 来源:2014-2015学年江西省九年级上学期第二次月考数学试卷(解析版) 题型:选择题
如图,在平面直角坐标系中,有一Rt△ ABC,且A(﹣1,3),B(﹣3,﹣1),C(﹣3,3),已知△A1AC1是由△ABC旋转得到的.则旋转中心的坐标是( ).
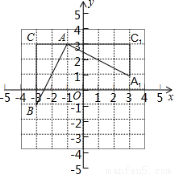
A.(0,0) B.(﹣1,0) C.(1,0) D.(0,﹣1)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级12月月考数学试卷(解析版) 题型:填空题
一个布袋里装有6个只有颜色可不同的球,其中2个红球,4个白球,从布袋里任意模出一个球,则模出的球是红球的概率为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级12月月考数学试卷(解析版) 题型:选择题
若从长度分别为3、5、6、9的四条线段中任取三条,则能组成三角形的概率为( ).
A.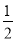 B.
B.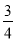 C.
C.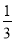 D.
D.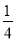
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省咸宁市中考模拟考试数学试卷(解析版) 题型:解答题
(本题满分8分) 为进一步促进青少年科技模型教育的普及和发展,丰富校园科技体育活动,某市6月份将举行中小学科技运动会。下图为某校将参加科技运动会航模比赛(包括空模、海模、车模、建模四个类别)的参赛人数统计图:
(1)该校参加航模比赛的总人数是 人,空模所在扇形的圆心角的度数是 ;
(2)把条形统计图补充完整;
(3)从全市中小学参加航模比赛选手中随机抽取80人,其中有32人获奖.今年该市中小学参加航模比赛人数共2485人,请你估算今年参加航模比赛的获奖人数约是多少人?



查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省咸宁市九年级上学期第四次月考数学试卷(解析版) 题型:解答题
已知关于x的一元二次方程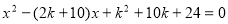 .
.
①证明该方程有两个不相等实根;
②若该方程两根刚好是一直角三角形两直角边长,且该直角三角形斜边为10,求k值。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市江都十校八年级12月联谊月考数学试卷(解析版) 题型:选择题
如图,把ABC经过一定的变换得到△A′B′C′,如果△ABC上点P的坐标为(x,y),那么这个点在△A′B′C′中的对应点P′的坐标为( )
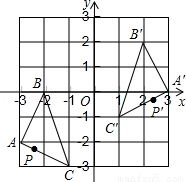
A.(﹣x,y﹣2)
B.(﹣x,y+2)
C.(﹣x+2,﹣y)
D.(﹣x+2,y+2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com