
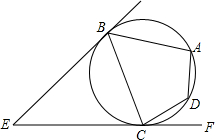
 如图,EB,EC是⊙O的两条切线,与⊙O相切于B,C两点,点A,D在圆上.若∠E=46°,∠DCF=32°,则∠A的度数是99°.
如图,EB,EC是⊙O的两条切线,与⊙O相切于B,C两点,点A,D在圆上.若∠E=46°,∠DCF=32°,则∠A的度数是99°. 分析 先根据切线长定理得到EB=EC,则∠ECB=∠EBC,于是可根据三角形内角和定理可计算出∠ECB=$\frac{1}{2}$(180°-∠E)=67°,接着利用平角的定义可计算出∠BCD=180°-∠ECB-∠DCF=81°,然后根据圆内接四边形的性质计算∠A的度数.
解答 解:∵EB,EC是⊙O的两条切线,
∴EB=EC,
∴∠ECB=∠EBC,
∴∠ECB=$\frac{1}{2}$(180°-∠E)=$\frac{1}{2}$×(180°-46°)=67°,
∴∠BCD=180°-∠ECB-∠DCF=180°-67°-32°=81°,
∵四边形ABCD为⊙O的内接四边形,
∴∠A+∠BCD=180°,
∴∠A=180°-81°=99°.
故答案为99.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径;从圆外一点引圆的切线,切线长相等.也考查了圆内接四边形的性质.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
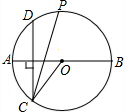 如图,AB为⊙O的直径,作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在下半圆上移动时,(不与点A、B重合),下列关于点P描述正确的是( )
如图,AB为⊙O的直径,作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在下半圆上移动时,(不与点A、B重合),下列关于点P描述正确的是( )| A. | 到CD的距离保持不变 | B. | 到D点距离保持不变 | ||
| C. | 等分$\widehat{BD}$ | D. | 位置不变 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
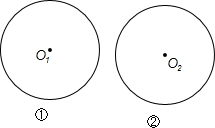 如图,所给两圆的圆心分别为O1,O2,半径都为3,根据要求完成作图(保留作图痕迹,不写作法).
如图,所给两圆的圆心分别为O1,O2,半径都为3,根据要求完成作图(保留作图痕迹,不写作法).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
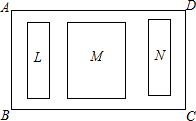 要对一块长60m,宽40m的矩形荒地ABCD(BC>AB)进行绿化和硬化.设计方案如图所示,矩形L、M、N为三块绿地,其余为硬化路面,L、M、N三块绿地周围的硬化路面宽都相等.并使三块绿地面积的和为矩形ABCD面积的$\frac{1}{2}$,求L、M、N三块绿地周围的硬化路面的宽.
要对一块长60m,宽40m的矩形荒地ABCD(BC>AB)进行绿化和硬化.设计方案如图所示,矩形L、M、N为三块绿地,其余为硬化路面,L、M、N三块绿地周围的硬化路面宽都相等.并使三块绿地面积的和为矩形ABCD面积的$\frac{1}{2}$,求L、M、N三块绿地周围的硬化路面的宽.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
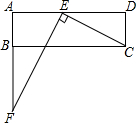 如图,在矩形ABCD中,已知AD>AB,在边AD上取点E,连结CE,过点E作EF⊥CE,与边AB的延长线交于点F.
如图,在矩形ABCD中,已知AD>AB,在边AD上取点E,连结CE,过点E作EF⊥CE,与边AB的延长线交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com