
【题目】如图,已知E、F是ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC. 
(1)求证:△ABE≌△CDF;
(2)请写出图中除△ABE≌△CDF外其余两对全等三角形(不再添加辅助线).
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠FCD,
又∵BE⊥AC,DF⊥AC,
∴∠AEB=∠CFD=90°,
∴△ABE≌△CDF(AAS)
(2)答:△ABC≌△CDA,△BCE≌△DAF
【解析】(1)根据平行四边形的性质得到AB=CD,AB∥CD,推出∠BAE=∠FCD,根据垂直的定义得到∠AEB=∠CFD=90°,根据AAS即可得到答案;(2)根据SSS得到△ABC≌△CDA,根据SAS得到△BCE≌△DAF.
【考点精析】解答此题的关键在于理解垂线的性质的相关知识,掌握垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短,以及对平行线的性质的理解,了解两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.


科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,AB=7,
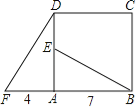
(1)指出旋转中心和旋转角度;
(2)求DE的长度;
(3)BE与DF的位置关系如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若单独租用一台车,租用哪台车合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民使用自来水按如下标准收费(水费按月缴纳):

(1)当a=2时,某用户一个月用了 28m3水,求该用户这个月应缴纳的水费;
(2)设某户月用水量为m立方米,当 m>20时,则该用户应缴纳的的水费为________元(用含 a、m的整式表示);
(3)当a=2时,甲、乙两用户一个月共用水 40m3,已知甲用户缴纳的水费超过了24元,设甲用户这个月用水xm3,试求甲、乙两用户一个月共缴纳的水费(用含 x的整式表示)。
查看答案和解析>>
科目:初中数学 来源: 题型:
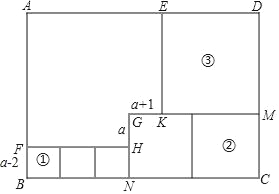
【题目】如图所示,用三种大小不等的正方形①②③和…个缺角的正方形拼成一个长方形ABCD(不重叠且没有缝隙),若GH=a,GK=a+1,BF=a﹣2
(1)试用含a的代数式表示:正方形②的边长CM的长= ,正方形③的边长DM的长= ;
(2)求长方形ABCD的周长(用含a的代数式表示);并求出当a=3时,长方形周长的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角△ABC中,∠BAC=90°,AC=AB,以AB为斜边在△ABC内部作Rt△ABD,连接CD,若∠ADC=135°,S△ABD=9,则线段AD的长度为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)某中学组织学生去福利院慰问,在准备礼品时发现,购买1个甲礼品比购买1个乙礼品多花40元,并且花费600元购买甲礼品和花费360元购买乙礼品的数量相等.
(1)求甲、乙两种礼品的单价各为多少元?
(2)学校准备购买甲、乙两种礼品共30个送给福利院的老人,要求购买礼品的总费用不超过2000元,那么最多可购买多少个甲礼品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:数轴上任意两点之间的距离与这两点对应的数的关系.
![]()
(1)如果点A表示数5,将点A先向左移动4个单位长度到达点B,那么点B表示的数是 ,A、B两点间的距离是 .
如果点A表示数﹣2,将点A向右移动5个单位长度到达点B,那么点B表示的数是 ,A、B两点间的距离是 .
(2)发现:在数轴上,如果点M对应的数是m,点N对应的数是n,那么点M与点N之间的距离可表示为 (用m、n表示,且m≥n).
(3)应用:利用你发现的结论解决下列问题:数轴上表示x和﹣2的两点P与Q之间的距离是3,则x= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪和小明沿同一条笔直的马路同时从学校出发到某图书馆查阅资料,学校与 图书馆的路程是 ![]() 千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到 达图书馆,图中折线
千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到 达图书馆,图中折线 ![]() 和线段
和线段 ![]() 分别表示两人离学校的路程
分别表示两人离学校的路程 ![]() (千米)与所经过的 时间
(千米)与所经过的 时间 ![]() (分钟)之间的函数关系,请根据图像回答下列问题:
(分钟)之间的函数关系,请根据图像回答下列问题:
(1)小聪在图书馆查阅资料的时间为 分钟;小聪返回学校的速度为 千米/分钟.
(2)请你求出小明离开学校的路程 ![]() (千米)与所经过的时间
(千米)与所经过的时间 ![]() (分钟)之间的函数表达式;
(分钟)之间的函数表达式;
(3)若设两人在路上相距不超过 ![]() 千米时称为可以“互相望见”,则小聪和小明可以“互相 望见”的时间共有多少分钟?
千米时称为可以“互相望见”,则小聪和小明可以“互相 望见”的时间共有多少分钟?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com