Question

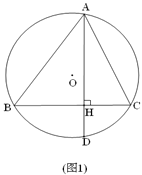
【题目】如图，△ABC内接于⊙O，弦AD⊥BC垂足为H，∠ABC＝2∠CAD.

（1）如图1，求证：AB＝BC；

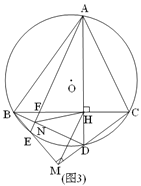
（2）如图2，过点B作BM⊥CD垂足为M，BM交⊙O于E,连接AE、HM，求证：AE∥HM;

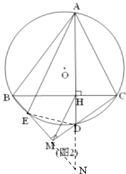
（3）如图3，在（2）的条件下，连接BD交AE于N，AE与BC交于点F，若NH＝2，AD＝11，求线段AB的长.

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）AB的长为10.

【解析】分析：（1）根据题意，设∠CAD=a，然后根据直角三角形的两锐角互余的关系，推导出∠BAC=∠ACB，再根据等角对等边得证结论；

（2）延长AD、BM交于点N，连接ED.根据圆周角定理得出∠N=∠DEN=∠BAN，进而根据等角对等边，得到DE=DN,BA=BN，再根据等腰三角形和直角三角形的性质，求得MH∥AE；

（3）连接CE，根据（2）的结论，由三角形全等的判定与性质证得HF=HC，然后结合勾股定理求出AC2-AH2=CD2-DH2，解得CD=5,CH=4,AH=8，最后根据锐角三角函数的性质得到AB.

详解：（1）证明：设∠CAD=a,

则∠ABC=2a,∠C=90°-a,∠BAD=90°-2a,

∴∠BAC=90°-2a+a=90°-a

∴∠BAC=∠ACB.∴AB=BC

(2）证明：延长AD、BM交于点N，连接ED.

∵∠DEN=∠DAB,∠N=∠BCD,∠BCD=∠BAN

∴∠N=∠DEN=∠BAN

∴DE=DN,BA=BN

又∵BH⊥AN,DM⊥EN

∴EM=NM,HN=HA,∴MH∥AE

（3）连接CE.

∠BDA=∠BCA,∠BDM=∠BAC,由（1）知∠BCA=∠BAC

∴∠BDA=∠BDM,∴△BDM≌△BDH,

∴DH=MH,∠MBD=∠HBD,∴BD⊥MH

又∵MH∥AE,∴BD⊥EF,∴△FNB≌△ENB,

同理可证△AFH≌△ACH,∴HF=HC,又∵FN=NE

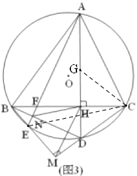
∴NH∥EC,EC=2NH,又∵NH=,∴EC=

∠EAC=2∠AEC=2a=∠ABC,可证弧AC=弧EC,

∴AC=EC=

设HD=x，AH=11-x，

∵∠ADC=2∠CAD,翻折△CHD至△CHG,可证CG=CD=AG

AH=CD+DH,CD=AH-DH=11-x-x=11-2x

又∵AC2-AH2=CD2-DH2,∴()2-(11-x)2=(11-2x)2-x2

∴x1=3,x2=(舍去)∴CD=5,CH=4,AH=8.

又∵,∴BH=6 ∴AB=