练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

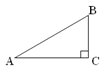
    【题目】如图，在Rt△ABC中，∠ACB=90°，∠BAC=30°，BC=2,在同一平面内，以AC为一边作等边△ACD，连接BD,则BD= ______．

    【答案】2或

    【解析】分析：根据题意，可分为在AC的下面和在AC的上面作等边三角形，两种情况，然后根据30°角的直角三角形和等边三角形的性质以及勾股定理求解即可.

    详解：根据题意，可分为D点在AC的下面：

    ∵∠BAC=30°，∠DAC=60°，

    ∴∠BAD=90°

    ∵∠BCA=90°

    ∴AB=2BC=4

    根据勾股定理可得AC=AD=2

    ∴在直角△ABD中，BD==2.

    点D在AC的上面，

    ∵∠DAC=60°，∠BAC=30°，△ACD是等边三角形，

    ∴AB垂直平分CD，

    ∴BD=BC=2.

    故答案为：2或.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】结合数轴与绝对值的知识回答下列问题：

    (1)数轴上表示4和1的两点之间的距离是 ；表示－3和2两点之间的距离是 ；一般地，数轴上表示数m和数n的两点之间的距离等于．如果表示数和－2的两点之间的距离是3，那么= ；

    (2)若数轴上表示数的点位于－4与2之间,求+的值；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】把几个图形拼成一个新的图形，再通过两种不同的方法计算同一个图形的面积，可以得到一个等式，也可以求出一些不规则图形的面积．

    例如，由图1，可得等式：（a+2b）（a+b）=a2+3ab+2b2

    （1）如图2，将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形，试用不同的形式表示这个大正方形的面积，你能发现什么结论？请用等式表示出来．

    （2）利用（1）中所得到的结论，解决下面的问题： 已知a+b+c=11，ab+bc+ac=38，求a2+b2+c2的值．

    （3）如图3，将两个边长分别为a和b的正方形拼在一起，B，C，G三点在同一直线上，连接BD和BF．若这两个正方形的边长满足a+b=10，ab=20，请求出阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读材料，根据材料回答：

    例如1：

    .

    例如2：

    8×0.125＝8×8×8×8×8×8×0.125×0.125×0.125×0.125×0.125×0.125

    ＝(8×0.125)×(8×0.125)×(8×0.125)×(8×0.125)×(8×0.125)×(8×0.125)

    ＝(8×0.125)6 ＝1.

    （1）仿照上面材料的计算方法计算：；

    （2）由上面的计算可总结出一个规律：(用字母表示) ；

    （3）用（2）的规律计算：.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】根据语句画图，并回答问题，如图，∠AOB内有一点P．

    （1）过点P画PC∥OB交OA于点C，画PD∥OA交OB于点D．

    （2）写出图中与∠CPD互补的角　 　．（写两个即可）

    （3）写出图中∠O相等的角　 　．（写两个即可）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将矩形ABCD沿对角线BD折叠，点C的对应点为点C′，连接CC′交AD于点F，BC′与AD交于点E．

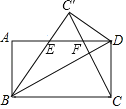
    （1）求证：△BAE≌△DC′E；

    （2）写出AE与EF之间的数量关系，并说明理由；

    （3）若CD＝2DF＝4，求矩形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，AB=12，AD=4，BC=9，点P是AB上一动点．若△PAD与△PBC是相似三角形，则满足条件的点P的个数有（　　）

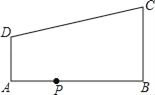
    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC内接于⊙O，弦AD⊥BC垂足为H，∠ABC＝2∠CAD.

    （1）如图1，求证：AB＝BC；

    （2）如图2，过点B作BM⊥CD垂足为M，BM交⊙O于E,连接AE、HM，求证：AE∥HM;

    （3）如图3，在（2）的条件下，连接BD交AE于N，AE与BC交于点F，若NH＝2，AD＝11，求线段AB的长.

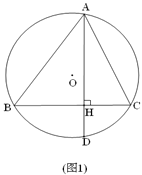
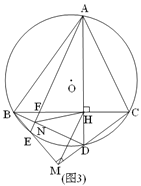
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】先化简，再求值：

    （1）a2＋（5a2－2a）－2（a2－3a），其中a＝－3．

    （2）已知∣2a＋1∣＋（b－1）2＝0，求：2（－a＋b2）＋（a－b2）－2（a＋b2）

    查看答案和解析>>

    同步练习册答案