
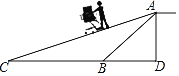
【题目】某购物超市为了方便顾客购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯,如图所示,已知原阶梯式自动扶梯AB的长为10m,∠ABD=45°,AD⊥直线BC于点D,改造后的斜坡式自动扶梯的坡角∠ACB=20°,求改造后的扶梯水平距离增加的部分BC的长度.(结果精确到0.1m,参考数据:sin20°≈0.35,cos20°≈0.94,tan20°≈0.37,![]() ≈1.41)
≈1.41)
科目:初中数学 来源: 题型:
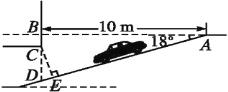
【题目】.某商场为缓解“停车难”问题,拟建造地下停车库,如图是该地下停车库坡道入口的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5 m.根据规定,地下停车库坡道入口上方要张贴限高标志,以便告知驾驶员所驾车辆能否安全驶入.小明认为CD的长就是所限制的高度,而小亮认为应该以CE的长作为限制的高度.小明和小亮谁说得对?请你判断并计算出正确的结果.(结果精确到0.1 m,参考数据:sin 18°≈0.31,cos 18°≈0.95,tan 18°≈0.325)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD表示该产品每千克生产成本y1(单位:元)与产量x(单位:kg)之间的函数关系;线段CD表示每千克的销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
(1)请解释图中点D的横坐标、纵坐标的实际意义.
(2)求线段AB所表示的y1与x之间的函数表达式.
(3)当0≤x≤90时,销售该产品获得的利润与产量的关系式是 ;当90≤x≤130时,销售该产品获得的利润与产量的关系式是 ;总之,当产量为 kg时,获得的利润最大,最大利润是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,Rt△ABC中,∠ACB=90°,AC=5,BC=12,点D在边AB上,以AD为直径的⊙O,与边BC有公共点E,则AD的最小值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a=4,b=5,则该矩形的面积为( )
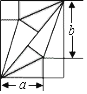
A.50B.40C.30D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC=3cm.动点P从点A出发,以![]() cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC
cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC![]() CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是 ( )
CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是 ( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC=![]() ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
(1)如图1,当点R与点D重合时,求PQ的长;
(2)如图2,试探索: ![]() 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于点P(a,b),若点P′的坐标为(![]() ,
,![]() )(其中k为常数,且k≠0),则称点P′为点P的“k关联点”.
)(其中k为常数,且k≠0),则称点P′为点P的“k关联点”.
(1)点P(﹣3,4)的“2关联点”P′的坐标是_______________;
(2)若a、b为正整数,点P的“k关联点”P′的坐标为(3,9),请直接写出k的值及点P的坐标;
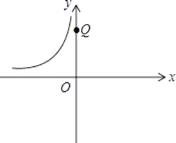
(3)如图,点Q的坐标为(0,2 ),点A在函数![]() 的图象上运动,且点A是点B的“﹣
的图象上运动,且点A是点B的“﹣![]() 关联点”,求线段BQ的最小值.
关联点”,求线段BQ的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com