
 按要求完成作图:
按要求完成作图:分析 ①利用关于y轴对称的点的坐标特征写出A1、B1、C1的坐标,然后描点即可得到△A1B1C1;
②用一个矩形的面积减去三个三角形的面积可计算出△ABC的面积.
解答 解:①如图,△A1B1C1为所作;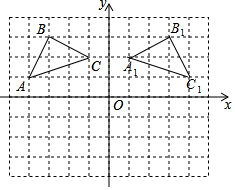
②S△ABC=3×2-$\frac{1}{2}$×3×1-$\frac{1}{2}$×2×1-$\frac{1}{2}$×2×1=2.5.
故答案为2.5.
点评 本题考查了作图-轴对称变换:画一个图形的轴对称图形时,也是先从确定一些特殊的对称点开始的,一般的方法是:由已知点出发向所给直线作垂线,并确定垂足;直线的另一侧,以垂足为一端点,作一条线段使之等于已知点和垂足之间的线段的长,得到线段的另一端点,即为对称点;连接这些对称点,就得到原图形的轴对称图形.记住关于坐标轴对称的点的坐标特征.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:填空题
 如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=2,则△A6B6A7的边长为64.
如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=2,则△A6B6A7的边长为64.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
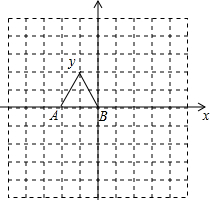 如图,在边长均为1的小正方形网格纸中,△OAB的顶点0、A、B均在格点上,且O是直角坐标系的原点,点A在x轴上.
如图,在边长均为1的小正方形网格纸中,△OAB的顶点0、A、B均在格点上,且O是直角坐标系的原点,点A在x轴上.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
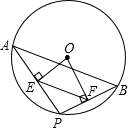 如图,点A、B是⊙O上两点,AB=16,点P是⊙O上的动点(P与A、B不重合)连接AP、PB,过点O分别作OE⊥AP于点E,OF⊥PB于点F,则EF=8.
如图,点A、B是⊙O上两点,AB=16,点P是⊙O上的动点(P与A、B不重合)连接AP、PB,过点O分别作OE⊥AP于点E,OF⊥PB于点F,则EF=8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线AB与y轴交于点A,与x轴交于点B,且∠BAO=30°,现将△OAB沿直线AB翻折,得到△CAB.连接OC交AB于点D.
如图,在平面直角坐标系中,直线AB与y轴交于点A,与x轴交于点B,且∠BAO=30°,现将△OAB沿直线AB翻折,得到△CAB.连接OC交AB于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com