
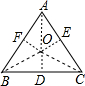
 解:过O做OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,连接OB、OA、OC,
解:过O做OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,连接OB、OA、OC,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
 美化城市、改善人们的居住环境已成为城市建设的一项重要内容.某区近几年来,通过拆迁旧房、植草、栽树、修建公园等措施,使城区绿地面积不断增加,根据图中所提供的信息,下列说法错误的是( )
美化城市、改善人们的居住环境已成为城市建设的一项重要内容.某区近几年来,通过拆迁旧房、植草、栽树、修建公园等措施,使城区绿地面积不断增加,根据图中所提供的信息,下列说法错误的是( )| A、2009年该区的绿地面积为420公顷 |
| B、2011年的绿地面积增长最快 |
| C、从2009年到2012年,每年绿地面积的增长率都在增长 |
| D、从2009年到2012年,每年的绿地面积都在增长 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com