
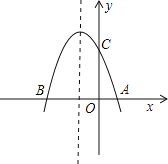
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.
【答案】(1)、y=-![]() -2x+3;(2)、Q(-1,2);(3)、(
-2x+3;(2)、Q(-1,2);(3)、(![]() ,
,![]() )
)
【解析】
试题分析:(1)、将点A和点B代入函数解析式,利用待定系数法求出函数解析式;(2)、根据题意得出A、B两点关于对称轴对称,则直线BC与x=-1的交点就是点Q,根据题意得出点C的坐标,然后利用待定系数法求出直线BC的解析式,从而得出点Q的坐标;(3)、首先设点P的坐标,然后根据△BPC的面积等于四边形BPCO的面积减去△BOC的面积,然后列出关于x的函数解析式,从而得出最大值.
试题解析:(1)、将A(1,0),B(﹣3,0)代y=﹣x2+bx+c中得
![]() ∴
∴![]() ∴抛物线解析式为:y=﹣x2﹣2x+3;
∴抛物线解析式为:y=﹣x2﹣2x+3;
(2)、存在
理由如下:由题知A、B两点关于抛物线的对称轴x=﹣1对称
∴直线BC与x=﹣1的交点即为Q点,此时△AQC周长最小∵y=﹣x2﹣2x+3 ∴C的坐标为:(0,3)
直线BC解析式为:y=x+3 Q点坐标即为![]() 解得
解得![]() ∴Q(﹣1,2);
∴Q(﹣1,2);
(3)、存在.
理由如下:设P点(x,﹣x2﹣2x+3)(﹣3<x<0) ∵S△BPC=S四边形BPCO﹣S△BOC=S四边形BPCO﹣![]()
若S四边形BPCO有最大值,则S△BPC就最大,
∴S四边形BPCO=S△BPE+S直角梯形PEOC=![]() BEPE+
BEPE+![]() OE(PE+OC)=
OE(PE+OC)=![]() (x+3)(﹣x2﹣2x+3)+
(x+3)(﹣x2﹣2x+3)+![]() (﹣x)(﹣x2﹣2x+3+3)
(﹣x)(﹣x2﹣2x+3+3)
=![]()
当x=﹣![]() 时,S四边形BPCO最大值=
时,S四边形BPCO最大值=![]() ∴S△BPC最大=
∴S△BPC最大=![]()
当x=﹣![]() 时,﹣x2﹣2x+3=
时,﹣x2﹣2x+3=![]() ∴点P坐标为(﹣
∴点P坐标为(﹣![]() ,
,![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】天上一颗颗闪烁的星星给我们以“_____”的形象;中国武术中有“枪扎一条线,棍扫一大片”的说法,这句话给我们以“_____”的形象;宾馆里旋转的大门给我们以“_____”的形象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次美化校园活动中,先安排32人去拔草,18人去植树,后又增派20人去支援他们,结果拔草的人数是植树人数的2倍、问支援拔草和支援植树的分别有多少人?若设支援拔草的有x人,则下列方程中正确的是( )
A.32+x=2×18
B.32+x=2(38﹣x)
C.52﹣x=2(18+x)
D.52﹣x=2×18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB,王华同学按下列步骤作图:(1)以点O为圆心,任意长为半径作弧,交OA于点C,交OB于点D,分别以点C、点D为圆心,大于![]() CD的长为半径作弧,两弧交于点E,作射线OE;(2)在射线OE上取一点F,分别以点O、点F为圆心,大于
CD的长为半径作弧,两弧交于点E,作射线OE;(2)在射线OE上取一点F,分别以点O、点F为圆心,大于![]() OF的长为半径作弧,两弧交于两点G、H,作直线GH,交OA于点M,交OB于点N;(3)连接FM、FN.那么四边形OMFN一定是( )
OF的长为半径作弧,两弧交于两点G、H,作直线GH,交OA于点M,交OB于点N;(3)连接FM、FN.那么四边形OMFN一定是( )
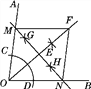
A. 梯形 B. 矩形 C. 菱形 D. 正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,ABCD中,点E,F在直线AC上(点E在F左侧),BE∥DF.

(1)求证:四边形BEDF是平行四边形;
(2)若AB⊥AC,AB=4,BC=![]() ,当四边形BEDF为矩形时,求线段AE的长.
,当四边形BEDF为矩形时,求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,晚上小明站在路灯P的底下观察自己的影子时发现,当他站在F点的位置时,在地面上的影子为BF,小明向前走2米到D点时,在地面上的影子为AD,若AB=4米,∠PBF=60°,∠PAB=30°,通过计算,求出小明的身高.(结果保留根号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com