
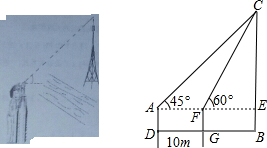
分析 在直角△EAC和直角△CEF中,根据三角函数可以用CE把AE、EF表示出来,根据AF=DG=30米,就可以得到一个关于CE的方程,求出CE的值,再根据AD的值,即可求出BC.
解答  解:在直角三角形EAC中,
解:在直角三角形EAC中,
∵∠EAC=45°,
∴AE=CE,
设CE=x米,
在直角三角形CEF中,
∵∠EFC=60°,
∴∠FCE=30°,
∴MN=CE•tan30°=$\frac{\sqrt{3}}{3}$x,
∵AF=DG=30米,
∴30+$\frac{\sqrt{3}}{3}$x=x,
解得:x=45+15$\sqrt{3}$,
∵AD=1米,
∴BC=BE+CE=46+15$\sqrt{3}$(米);
答:这个信号发射塔的高度为(46+15$\sqrt{3}$)米.
点评 本题主要考查了解直角三角的应用-仰角俯角,用到的知识点是三角函数的定义,根据三角函数可以把问题转化为方程问题来解决是关键.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:解答题
 完成下列推理填空:
完成下列推理填空:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
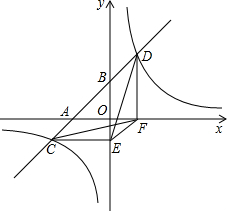 如图,直线l与x轴、y轴交于A、B两点.与双曲线y=$\frac{k}{x}$和交于C、D两点,分别过C、D两点作y轴,x轴的垂线,垂足为E、F.连接CF、DE.则下列结论中:
如图,直线l与x轴、y轴交于A、B两点.与双曲线y=$\frac{k}{x}$和交于C、D两点,分别过C、D两点作y轴,x轴的垂线,垂足为E、F.连接CF、DE.则下列结论中:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com