
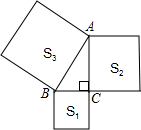
 如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1、S2、S3,且S1=10,S2=15,则AB的长为5.
如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1、S2、S3,且S1=10,S2=15,则AB的长为5.  浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=3x+2 | B. | y=-3x-2 | C. | y=-3(x+2) | D. | y=-3(x-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
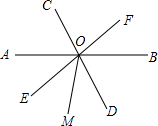 如图,直线AB,CD,EF相交于点O,∠BOD=64°,∠AOF=140°.
如图,直线AB,CD,EF相交于点O,∠BOD=64°,∠AOF=140°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
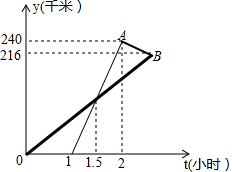 十一期间,小明和小亮相约从长春出发到某市某游乐园游玩,小明乘私家车从长春出发1小时后,小亮乘“和谐号”动车从长春出发,先到某市火车站A,然后乘出租车去游乐园B(换车时间忽略不计),两人恰好同时到达游乐园,他们离开长春的距离y(千米)与小明乘车时间t(时)的函数图象如图所示.
十一期间,小明和小亮相约从长春出发到某市某游乐园游玩,小明乘私家车从长春出发1小时后,小亮乘“和谐号”动车从长春出发,先到某市火车站A,然后乘出租车去游乐园B(换车时间忽略不计),两人恰好同时到达游乐园,他们离开长春的距离y(千米)与小明乘车时间t(时)的函数图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com