
【题目】如图,在△ABC中,AB=BC,CD⊥AB于点D,CD=BD,BE平分∠ABC,点H是BC边的中点,连接DH,交BE于点G,连接CG. 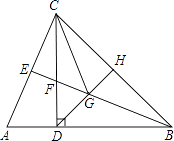
(1)求证:△ADC≌△FDB;
(2)求证:CE= ![]() BF;
BF;
(3)判断△ECG的形状,并证明你的结论;
(4)猜想BG与CE的数量关系,并证明你的结论.
【答案】
(1)证明:∵AB=BC,BE平分∠ABC,
∴BE⊥AC,CE=AE,
∵CD⊥AB,
∴∠ACD=∠DBF,
在△ADC和△FDB中,
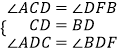 ,
,
∴△ADC≌△FDB(ASA);
(2)证明:∵△ADC≌△FDB,
∴AC=BF,
又∵CE=AE,
∴CE= ![]() BF;
BF;
(3)证明:△ECG为等腰直角三角形.
∵点H是BC边的中点,
∴GH垂直平分BC,
∴GC=GB,
∵∠DBF=∠GBC=∠GCB=∠ECF,得∠ECG=45°,
又∵BE⊥AC,
∴△ECG为等腰直角三角形;
(4)证明:GB= ![]() CE;
CE;
∵△ECG为等腰直角三角形,
∴GC= ![]() CE,
CE,
∵GC=GB,
∴GB= ![]() CE.
CE.
【解析】(1)首先根据AB=BC,BE平分∠ABC,得到BE⊥AC,CE=AE,进一步得到∠ACD=∠DBF,结合CD=BD,即可证明出△ADC≌△FDB;(2)由△ADC≌△FDB得到AC=BF,结合CE=AE,即可证明出结论;(3)由点H是BC边的中点,得到GH垂直平分BC,即GC=GB,由∠DBF=∠GBC=∠GCB=∠ECF,得∠ECO=45°,结合BE⊥AC,即可判断出△ECG的形状;(4)由△ECG为等腰直角三角形,得到GC= ![]() CE,因为GC=GB,即可得到GB=
CE,因为GC=GB,即可得到GB= ![]() CE.
CE.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(m-2)x2-4x-2=0有两个实数根,则实数m的取值范围是( )
A. m≥0B. m>0C. m≥0,m≠2D. m>0,m≠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF.
(1)求证:AB是⊙O的切线;
(2)若CF=4,DF=![]() ,求⊙O的半径r及sinB.
,求⊙O的半径r及sinB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
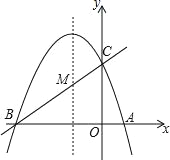
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E、F分别在BC、AD上,且∠BAE=∠DCF.
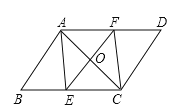
(1)求证:△ABE≌△CDF;
(2)若AC⊥EF,试判断四边形AECF是什么特殊四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2014年南京青奥会某项目6名礼仪小姐的身高如下(单位:cm):168,166,168,167,169,168,则她们身高的众数是cm,极差是cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com