
如图,直线y=- x+6分别与x轴、y轴交于A、B两点;直线y=
x+6分别与x轴、y轴交于A、B两点;直线y= x与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿
x与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿 轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN,设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为t(秒).
轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN,设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为t(秒).

(1)求点C的坐标;
(2)当0<t<5时,求S与t之间的函数关系式,并求S的最大值;
(3)当t>0时,直接写出点(4,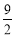 )在正方形PQMN内部时t的取值范围.
)在正方形PQMN内部时t的取值范围.
(1)(3, );(2)当0<t≤
);(2)当0<t≤ 时,S=-2(t-
时,S=-2(t- )2+
)2+ ,当
,当 ≤t<5时,S=4(t-5)2,
≤t<5时,S=4(t-5)2, ;(3)
;(3)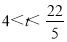 .
.
【解析】
试题分析:(1)利用已知函数解析式,求两直线的交点,得点C的坐标即可;
(2)根据几何关系把s用t表示,注意当MN在AD上时,这一特殊情况,进而分类讨论得出;
(3)利用(2)中所求,结合二次函数最值求法求出即可.
试题解析: (1)由题意,得
 ,解得:
,解得: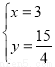 ,
,
∴C(3, );
);
(2)∵直线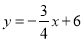 分别与x轴、y轴交于A、B两点,
分别与x轴、y轴交于A、B两点,
∴y=0时, ,解得;x=8,
,解得;x=8,
∴A点坐标为;(8,0),
根据题意,得AE=t,OE=8-t.
∴点Q的纵坐标为 (8-t),点P的纵坐标为-
(8-t),点P的纵坐标为- (8-t)+6=
(8-t)+6= t,
t,
∴PQ= (8-t)-
(8-t)- t=10-2t.
t=10-2t.
当MN在AD上时,10-2t=t,
∴t= .
.
当0<t≤ 时,S=t(10-2t),即S=-2t2+10t.
时,S=t(10-2t),即S=-2t2+10t.
当 <t<5时,S=(10-2t)2,即S=4t2-40t+100;
<t<5时,S=(10-2t)2,即S=4t2-40t+100;
当0<t≤ 时,S=-2(t-
时,S=-2(t- )2+
)2+ ,
,
∴t= 时,S最大值=
时,S最大值= .
.
当 ≤t<5时,S=4(t-5)2,
≤t<5时,S=4(t-5)2,
∵t<5时,S随t的增大而减小,
∴t= 时,S最大值=
时,S最大值=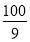 .
.
∵ >
>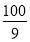 ,
,
∴S的最大值为 .
.
(3)点(4, )在正方形PQMN内部时t的取值范围是
)在正方形PQMN内部时t的取值范围是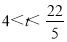 .
.
考点: 一次函数综合题.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源:2013-2014学年新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习三十五讲练习卷(解析版) 题型:填空题
如图,△ABC的一边AB是⊙O的直径,请你添加一个条件,使BC是⊙O的切线,你所添加的条件为________.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习三十三讲练习卷(解析版) 题型:解答题
如图某天上午9时,向阳号轮船位于A处,观测到某港口城市P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到城市P位于该船的南偏西36.9°方向,求此时轮船所处位置B与城市P的距离?(参考数据:sin 36.9°≈ ,tan 36.9°≈
,tan 36.9°≈ ,sin 67.5°≈
,sin 67.5°≈ ,tan 67.5°≈
,tan 67.5°≈ )
)

查看答案和解析>>
科目:初中数学 来源:2013-2014学年新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习三十一讲练习卷(解析版) 题型:解答题
(1)如图1,在△ABC中,BA=BC,D,E是AC边上的两点,且满足∠DBE= ∠ABC(0°<∠CBE<
∠ABC(0°<∠CBE< ∠ABC),以点B为旋转中心,将△BEC按逆时针旋转,得到△BE′A(点C与点A重合,点E到点E′处)连接DE′.
∠ABC),以点B为旋转中心,将△BEC按逆时针旋转,得到△BE′A(点C与点A重合,点E到点E′处)连接DE′.

求证:DE′=DE.
(2)如图2,在△ABC中,BA=BC,∠ABC=90°,D,E是AC边上的两点,且满足∠DBE= ∠ABC(0°<∠CBE<∠45°).
∠ABC(0°<∠CBE<∠45°).
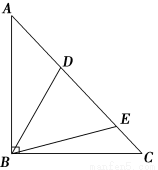
求证:DE2=AD2+EC2.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习三十一讲练习卷(解析版) 题型:选择题
如图,这是一个正面为黑,反面为白的未拼完的拼木盘,给出如下四块正面为黑、反面为白的拼木,现欲拼满拼木盘并使其颜色一致,请问应选择的拼木是( )


查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东省深圳市石岩公学九年级3月质量检测数学试卷(解析版) 题型:选择题
下列命题是真命题的有( )
①对角线相等的四边形是矩形;②两直线平行,同位角相等;③若AO=OB,则点O是AB的中点;④对角线相等的梯形是等腰梯形;⑤平分弦的直径垂直于弦,并且平分弦所对的弧。
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com