
ЁОЬтФПЁПОиаЮAOBCжаЃЌOBЃН8ЃЌOAЃН4ЃЎЗжБ№вдOBЃЌOAЫљдкжБЯпЮЊxжсЃЌyжсЃЌНЈСЂШчЭМ1ЫљЪОЕФЦНУцжБНЧзјБъЯЕЃЎFЪЧBCБпЩЯвЛИіЖЏЕуЃЈВЛгыBЃЌCжиКЯЃЉЃЌЙ§ЕуFЕФЗДБШР§КЏЪ§yЃН![]() ЃЈkЃО0ЃЉЕФЭМЯѓгыБпACНЛгкЕуEЃЎ
ЃЈkЃО0ЃЉЕФЭМЯѓгыБпACНЛгкЕуEЃЎ
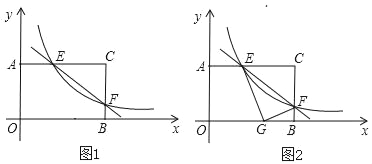
ЃЈ1ЃЉЕБЕуFдЫЖЏЕНБпBCЕФжаЕуЪБЃЌЧѓЕуEЕФзјБъЃЛ
ЃЈ2ЃЉСЌНгEFЁЂABЃЌЧѓжЄЃКEFЁЮABЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌНЋЁїCEFбиEFелЕўЃЌЕуCЧЁКУТфдкБпOBЩЯЕФЕуGДІЃЌЧѓДЫЪБЗДБШР§КЏЪ§ЕФНтЮіЪНЃЎ
ЁОД№АИЁПЃЈ1ЃЉEЃЈ4ЃЌ4ЃЉЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉyЃН![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЪзЯШШЗЖЈЕуFзјБъЃЌЧѓГіЗДБШР§КЏЪ§НтЮіЪНЃЌдйИљОнНтЮіЪНЧѓЕУЕуEзјБъМДПЩЃЛ
ЃЈ2ЃЉСЌНгABЃЌЗжБ№ЧѓГіЁЯEFCЃЌЁЯABCЕФе§ЧажЕМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉЯШзїГіИЈжњЯпХаЖЯГіRtЁїMEGЁзRtЁїBGFЃЌдйШЗЖЈГіЕуEЃЌFзјБъНјЖјEGЃН8Љ![]() ЃЌGFЃН4Љ
ЃЌGFЃН4Љ![]() ЃЌЧѓГіBDЃЌзюКѓгУЙДЙЩЖЈРэНЈСЂЗНГЬЧѓГіkМДПЩЕУГіНсТлЃЛ
ЃЌЧѓГіBDЃЌзюКѓгУЙДЙЩЖЈРэНЈСЂЗНГЬЧѓГіkМДПЩЕУГіНсТлЃЛ
НтЃКЃЈ1ЃЉЁпЫФБпаЮOACBЪЧОиаЮЃЌOBЃН8ЃЌOAЃН4ЃЌ
ЁрCЃЈ8ЃЌ4ЃЉЃЌ
ЁпЕуFЪЧBCжаЕуЃЌ
ЁрFЃЈ8ЃЌ2ЃЉЃЌ
ЁпЕуFдкyЃН![]() ЩЯЃЌ
ЩЯЃЌ
Ёрk=16ЃЌЗДБШР§КЏЪ§НтЮіЪНЮЊyЃН![]()
ЁпЕуEдкЗДБШР§КЏЪ§ЭМЯёЩЯЃЌЧвEЕуЕФзнзјБъЮЊ4ЃЌ
Ёр4ЃН![]()
Ёрx=4
ЁрEЃЈ4ЃЌ4ЃЉЃЎ
ЃЈ2ЃЉСЌНгABЃЌЩшЕуFЃЈ8ЃЌaЃЉЃЌ

ЁрkЃН8aЃЌ
ЁрEЃЈ2aЃЌ4ЃЉЃЌ
ЁрCFЃН4ЉaЃЌECЃН8Љ2aЃЌ
дкRtЁїECFжаЃЌtanЁЯEFCЃН![]() ЃН2ЃЌ
ЃН2ЃЌ
дкRtЁїACBжаЃЌtanЁЯABCЃН![]() ЃН2ЃЌ
ЃН2ЃЌ
ЁрtanЁЯEFCЃНtanЁЯABCЃЌ
ЁрЁЯEFCЃНЁЯABCЃЌ
ЁрEFЁЮABЃЎ
ЃЈ3ЃЉШчЭМЃЌ
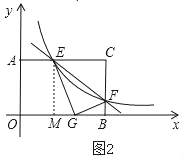
ЩшНЋЁїCEFбиEFелЕўКѓЃЌЕуCЧЁКУТфдкOBЩЯЕФGЕуДІЃЌ
ЁрЁЯEGFЃНЁЯCЃН90ЁуЃЌECЃНEGЃЌCFЃНGFЃЌ
ЁрЁЯMGE+ЁЯFGBЃН90ЁуЃЌ
Й§ЕуEзїEMЁЭOBЃЌ
ЁрЁЯMGE+ЁЯMEGЃН90ЁуЃЌ
ЁрЁЯMEGЃНЁЯFGBЃЌ
ЁрRtЁїMEGЁзRtЁїBGFЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпЕуEЃЈ![]() ЃЌ4ЃЉЃЌFЃЈ8ЃЌ
ЃЌ4ЃЉЃЌFЃЈ8ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрECЃНACЉAEЃН8Љ![]() ЃЌCFЃНBCЉBFЃН4Љ
ЃЌCFЃНBCЉBFЃН4Љ![]() ЃЌ
ЃЌ
ЁрEGЃНECЃН8Љ![]() ЃЌGFЃНCFЃН4Љ
ЃЌGFЃНCFЃН4Љ![]() ЃЌ
ЃЌ
ЁпEMЃН4ЃЌ
Ёр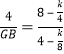 ЃЌ
ЃЌ
ЁрGBЃН2ЃЌ
дкRtЁїGBFжаЃЌGF2ЃНGB2+BF2ЃЌ
МДЃКЃЈ4Љ![]() ЃЉ2ЃНЃЈ2ЃЉ2+ЃЈ
ЃЉ2ЃНЃЈ2ЃЉ2+ЃЈ![]() ЃЉ2ЃЌ
ЃЉ2ЃЌ
ЁрkЃН12ЃЌ
ЁрЗДБШР§КЏЪ§БэДяЪНЮЊyЃН![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛЮЛдЫЖЏдБдкОрРКЯТ4mДІЬјЦ№ЭЖРКЃЌЧђдЫааЕФТЗЯпЪЧХзЮяЯпЃЌЕБЧђдЫааЕФЫЎЦНОрРыЪЧ2.5mЪБЃЌДяЕНзюДѓИпЖШ3.5mЃЌШЛКѓзМШЗТфШыРКШІЃЎвбжЊРКШІжааФЕНЕиУцЕФОрРыЮЊ3.05mЃЎ
ЃЈ1ЃЉНЈСЂШчЭМЫљЪОЕФЦНУцжБНЧзјБъЯЕЃЌЧѓХзЮяЯпЕФНтЮіЪНЃЎ
ЃЈ2ЃЉИУдЫЖЏдБЩэИп1.8mЃЌдкетДЮЬјЭЖжаЃЌЧђдкЭЗЖЅЩЯ0.25mДІГіЪжЃЌ
ЮЪЃКЧђГіЪжЪБЃЌЫћОрРыЕиУцЕФИпЖШЪЧЖрЩйЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТУцВФСЯЃЌШЛКѓНтД№ЮЪЬтЃК
дкЦНУцжБНЧзјБъЯЕжаЃЌвдШЮвтСНЕуPЃЈx1ЃЌy1ЃЉЃЌQЃЈx2ЃЌy2ЃЉЮЊЖЫЕуЕФЯпЖЮЕФжаЕузјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЫЋЧњЯпyЃН
ЃЉЃЎШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЫЋЧњЯпyЃН![]() ЃЈxЃМ0ЃЉКЭyЃН
ЃЈxЃМ0ЃЉКЭyЃН![]() ЃЈxЃО0ЃЉЕФЭМЯѓЙигкyжсЖдГЦЃЌжБЯпyЃН
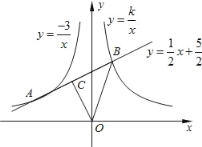
ЃЈxЃО0ЃЉЕФЭМЯѓЙигкyжсЖдГЦЃЌжБЯпyЃН![]() гыСНИіЭМЯѓЗжБ№НЛгкAЃЈaЃЌ1ЃЉЃЌBЃЈ1ЃЌbЃЉСНЕуЃЌЕуCЮЊЯпЖЮABЕФжаЕуЃЌСЌНгOCЁЂOBЃЎ
гыСНИіЭМЯѓЗжБ№НЛгкAЃЈaЃЌ1ЃЉЃЌBЃЈ1ЃЌbЃЉСНЕуЃЌЕуCЮЊЯпЖЮABЕФжаЕуЃЌСЌНгOCЁЂOBЃЎ
ЃЈ1ЃЉЧѓaЁЂbЁЂkЕФжЕМАЕуCЕФзјБъЃЛ
ЃЈ2ЃЉШєдкзјБъЦНУцЩЯгавЛЕуDЃЌЪЙЕУвдOЁЂCЁЂBЁЂDЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌЧыЧѓГіЕуDЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкСтаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌЖдНЧЯп
ЃЌЖдНЧЯп![]() ЦНЗжНЧ
ЦНЗжНЧ![]() ЃЌЕу
ЃЌЕу![]() ЪЧ
ЪЧ![]() ФквЛЕуЃЌСЌНг
ФквЛЕуЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌШє
ЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌдђСтаЮ
ЃЌдђСтаЮ![]() ЕФУцЛ§ЕШгк_____________ЃЎ
ЕФУцЛ§ЕШгк_____________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
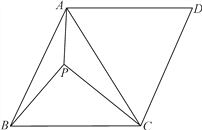
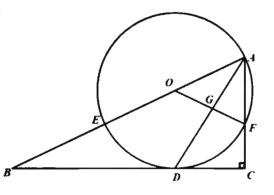
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЦНЗж
ЦНЗж![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() ЩЯвЛЕуЃЌОЙ§Еу
ЩЯвЛЕуЃЌОЙ§Еу![]() ЃЌ
ЃЌ![]() ЕФ
ЕФ![]() ЗжБ№НЛ
ЗжБ№НЛ![]() ЃЌ
ЃЌ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ЃЌСЌНг
ЃЌСЌНг![]() НЛ
НЛ![]() гкЕу
гкЕу![]() .
.
ЃЈ1ЃЉЧѓжЄЃК![]() ЪЧ
ЪЧ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
ЃЈ2ЃЉЩш![]() ЃЌ
ЃЌ![]() ЃЌЪдгУКЌ
ЃЌЪдгУКЌ![]() ЕФДњЪ§ЪНБэЪОЯпЖЮ
ЕФДњЪ§ЪНБэЪОЯпЖЮ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ3ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄ.
ЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжЊЙигкxЕФЗНГЬx2+2(a-1)x+a2-7a-4=0ЕФИљЮЊx1ЃЌx2ЃЌЧвТњзуx1x2-3x1-3x2-2=0ЃЌЧѓ![]()
![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТБэжагаСНжжвЦЖЏЕчЛАМЦЗбЗНЪНЃЎ
дТЪЙгУЗб | жїНаЯоЖЈЪБМф | жїНаГЌЪБЗб | БЛНа | |
ЗНЪНвЛ | 49 | 100 |
| УтЗб |
ЗНЪНЖў | 69 | 150 |
| УтЗб |
ЩшвЛИідТФкжїНаЭЈЛАЮЊtЗжжг![]() ЪЧе§ећЪ§
ЪЧе§ећЪ§![]() ЃЎ
ЃЎ
![]() ЕБ
ЕБ![]() ЪБЃЌАДЗНЪНвЛМЦЗбЮЊ______дЊЃЛАДЗНЪНЖўМЦЗбЮЊ______дЊЃЛ
ЪБЃЌАДЗНЪНвЛМЦЗбЮЊ______дЊЃЛАДЗНЪНЖўМЦЗбЮЊ______дЊЃЛ
![]() ЕБ
ЕБ![]() ЪБЃЌЪЧЗёДцдкФГвЛЪБМфtЃЌЪЙСНжжМЦЗбЗНЪНЯрЕШЃЌШєДцдкЃЌЧыЧѓГіЖдгІtЕФжЕЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЪБЃЌЪЧЗёДцдкФГвЛЪБМфtЃЌЪЙСНжжМЦЗбЗНЪНЯрЕШЃЌШєДцдкЃЌЧыЧѓГіЖдгІtЕФжЕЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
![]() ЕБ
ЕБ![]() ЪБЃЌЧыжБНгаДГіЪЁЧЎЕФМЦЗбЗНЪНЃП
ЪБЃЌЧыжБНгаДГіЪЁЧЎЕФМЦЗбЗНЪНЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌRtЁїABCжаЃЌЁЯABC=90ЁуЃЌЕуDЃЌFЗжБ№ЪЧACЃЌABЕФжаЕуЃЌCEЁЮDBЃЌBEЁЮDCЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮDBECЪЧСтаЮЃЛ
ЃЈ2ЃЉШєAD=3ЃЌDF=1ЃЌЧѓЫФБпаЮDBECУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
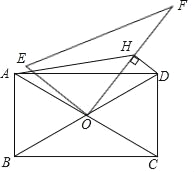
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌABЃН4ЃЌBCЃН4![]() ЃЌЖдНЧЯпACЁЂBDЯрНЛгкЕуOЃЌЯжНЋвЛИіжБНЧШ§НЧАхOEFЕФжБНЧЖЅЕугыOжиКЯЃЌдйШЦзХOЕузЊЖЏШ§НЧАхЃЌВЂЙ§ЕуDзїDHЁЭOFгкЕуHЃЌСЌНгAHЃЎдкзЊЖЏЕФЙ§ГЬжаЃЌAHЕФзюаЁжЕЮЊ_____ЃЎ
ЃЌЖдНЧЯпACЁЂBDЯрНЛгкЕуOЃЌЯжНЋвЛИіжБНЧШ§НЧАхOEFЕФжБНЧЖЅЕугыOжиКЯЃЌдйШЦзХOЕузЊЖЏШ§НЧАхЃЌВЂЙ§ЕуDзїDHЁЭOFгкЕуHЃЌСЌНгAHЃЎдкзЊЖЏЕФЙ§ГЬжаЃЌAHЕФзюаЁжЕЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com