
【题目】如图,抛物线![]() 与两坐标轴相交于点
与两坐标轴相交于点![]() ,
,![]() 是抛物线的顶点,
是抛物线的顶点, ![]() 是线段
是线段![]() 的中点.
的中点.
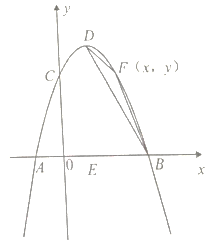
(1)求抛物线的解析式,并写出![]() 点的坐标;
点的坐标;
(2) ![]() 是抛物线上的动点;
是抛物线上的动点;
①当![]() 时,求
时,求![]() 的面积的最大值;
的面积的最大值;
②当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
【答案】(1)y=-x2+2x+3,D(1,4); (2) ①当x=2时,S最大值=1;②F(-![]() ,-2
,-2![]() -2)或(2-
-2)或(2-![]() ,-2+2
,-2+2![]() )
)
【解析】(1)利用待定系数法可求得抛物线的解析式,然后再配方成顶点式即可得点D的坐标;
(2)①由x>1,y>0,可以确定点F是直线BD上方抛物线上的动点,F(x, -x2+2x+3),过点F作FH⊥x轴交直线BD于M,由B、D的坐标易得yBD=-2x+6,继而得M(x,-2x+6),从而得到FM=-(x-2)2+1,再根据S△BDF=S△DFM+S△BFM,从而可得S△BDF=-(x-2)2+1,根据二次函数的性质即可得;
②分点F在x轴上方抛物线上,点F在x轴下方、y轴左侧抛物线上两种情况进行讨论即可得.
(1)抛物线![]() 与两坐标轴相交于点
与两坐标轴相交于点![]()
由题意得: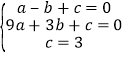 ,解得:
,解得: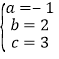 ,
,
所以抛物线的解析式为:y=-x2+2x+3,
配方得 y=-(x-1)2+4,∴抛物线顶点D的坐标为(1,4);
(2) ①∵x>1,y>0,
∴点F是直线BD上方抛物线上的动点,
则F(x, -x2+2x+3),
如图,过点F作FH⊥x轴交直线BD于M,
∵B(3,0), D(1,4),
∴yBD=-2x+6,
则M(x,-2x+6),
∴FM=-x2+2x+3-(-2x+6)= -x2+4x-3=-(x-2)2+1,
∵S△BDF=S△DFM+S△BFM,
∴S△BDF=![]() FM(x-1)+
FM(x-1)+![]() FM(3-x)=
FM(3-x)=![]() FM(x-1+3-x)=FM =-(x-2)2+1,
FM(x-1+3-x)=FM =-(x-2)2+1,
∴当x=2时,S最大值=1;
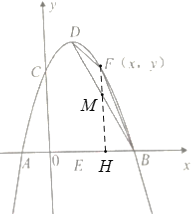
②如图,当 FE∥BD,且点F在x轴上方抛物线上时,
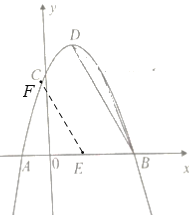
设FE的解析式为y=-2x+b,
∵直线FE过点E(1,0),
∴b=2,
yFE=-2x+2,
联立y=-2x+2与y=-x2+2x+3,
解得F(2-![]() ,-2+2
,-2+2![]() );
);
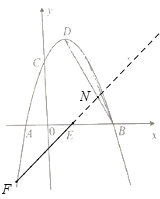
如图,当F在x轴下方、y轴左侧抛物线上时,设直线EF与直线BD交于点N,
∵∠AEF=∠NEB,
又∵∠AEF=∠
∴∠NEB=∠DBE,
∴NE=NB,
∴点N的横坐标为2,
又∵点N在直线yBD=-2x+6上,
∴N(2,2),
∴yEN=2x-2,
联立y=2x-2与y=-x2+2x+3,
解得F(-![]() ,-2
,-2![]() -2),
-2),
综上所述F(-![]() ,-2
,-2![]() -2)或(2-
-2)或(2-![]() ,-2+2
,-2+2![]() ).
).


科目:初中数学 来源: 题型:
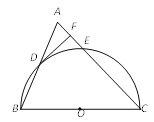
【题目】(9分)如图,△ABC为等腰三角形,AC=BC,以边BC为直径的半圆与边AB,AC分别交于D,E两点,过点D作DF⊥AC,垂足为点F.
(1)判断DF与⊙O的位置关系,并证明你的结论;
(2)若BC=9,EF=1,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知含字母a,b的代数式是:3[a2+2(b2+ab﹣2)]﹣3(a2+2b2)﹣4(ab﹣a﹣1)
(1)化简代数式;
(2)小红取a,b互为倒数的一对数值代入化简的代数式中,恰好计算得代数式的值等于0,那么小红所取的字母b的值等于多少?
(3)聪明的小刚从化简的代数式中发现,只要字母b取一个固定的数,无论字母a取何数,代数式的值恒为一个不变的数,那么小刚所取的字母b的值是多少呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B分别为数轴上的两点,A点对应的数为﹣20,B点对应的数为100.
![]()
(1)请写出与A,B两点距离相等的点M所对应的数 .
(2)现有一只电子蚂蚁P从B点出发,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度向右运动,x秒后两只电子蚂蚁在数轴上的C点相遇,请列方程求出x,并指出点C表示的数.
(3)若当电子蚂蚁P从B点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度也向左运动,y秒后两只电子蚂蚁在数轴上的D点相遇,请列方程求出y并指出点D表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P从(0,3)出发,沿所示的方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点p第2019次碰到矩形的边时点P的坐标为( )
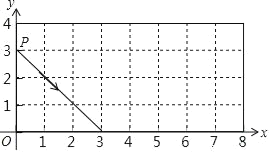
A. ( 1,4 )B. ( 5,0 )C. ( 8,3 )D. ( 6,4 )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某公园设计节日鲜花摆放方案,其中一个花坛由一批花盆堆成六角垛,顶层一个,以下各层堆成六边形,逐层每边增加一个花盆,若这垛花盆底层最长的一排共13个花盆,则底层的花盆的个数是( )
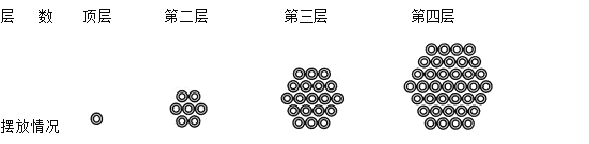
A.91B.127C.169D.255
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,点A是![]() 轴正半轴上一个定点,点P是函数
轴正半轴上一个定点,点P是函数![]() (
(![]() >0)上一个动点,PB⊥
>0)上一个动点,PB⊥![]() 轴于点B,连结PA,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
轴于点B,连结PA,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
A. 逐渐增大 B. 先增后减 C. 逐渐减小 D. 先减后增
查看答案和解析>>
科目:初中数学 来源: 题型:
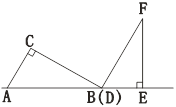
【题目】两个三角板ABC,DEF按如图所示的位置摆放,点B与点D重合,边AB与边DE在同一条直线上(假设图形中所有的点、线都在同一平面内),其中,∠C=∠DEF=90°,∠ABC=∠F=30°,AC=DE=4 cm.现固定三角板DEF,将三角板ABC沿射线DE方向平移,当点C落在边EF上时停止运动.设三角板平移的距离为![]() (cm),两个三角板重叠部分的面积为
(cm),两个三角板重叠部分的面积为![]() (cm2).
(cm2).
(1)当点C落在边EF上时,![]() =________cm;
=________cm;
(2)求![]() 关于
关于![]() 的函数表达式,并写出自变量
的函数表达式,并写出自变量![]() 的取值范围;
的取值范围;
(3)设边BC的中点为点M,边DF的中点为点N,直接写出在三角板平移过程中,点M与点N之间距离的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(2,0),B ( 2,0),C为 y 轴负半轴上一点,D是第四象限内一动点,且始终有BDA 2ACO 成立,过C 点作CE BD 于点 E .
(1)求证:DAC DBC ;
(2)若点 F 在 AD 的延长线上,求证:CD 平分BDF ;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com