
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.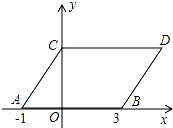
(1)求点C,D的坐标;
(2)若在y轴上存在点 M,连接MA,MB,使S△MAB=S平行四边形ABDC , 求出点M的坐标.
(3)若点P在直线BD上运动,连接PC,PO.
①若P在线段BD之间时(不与B,D重合),求S△CDP+S△BOP的取值范围;
②若P在直线BD上运动,请直接写出∠CPO、∠DCP、∠BOP的数量关系.
【答案】
(1)解:由平移可知:C(0,2),D(4,2);
(2)解:∵AB=4,CO=2,
∴S平行四边形ABOC=ABCO=4×2=8,
设M坐标为(0,m),
∴ ![]() ×4×|m|=8,解得m=±4
×4×|m|=8,解得m=±4
∴M点的坐标为(0,4)或(0,﹣4);
(3)解:①S梯形OCDB= ![]() ×(3+4)×2=7,
×(3+4)×2=7,
当点P运动到点B时,S△BOC最小,S△BOC的最小值= ![]() ×3×2=3,S△CDP+S△BOP<4,
×3×2=3,S△CDP+S△BOP<4,
当点P运动到点D时,S△BOC最大,S△BOC的最大值= ![]() ×4×2=4,S△CDP+S△BOP>3,
×4×2=4,S△CDP+S△BOP>3,
所以3<S△CDP+S△BOP<4;
②当点P在BD上,如图1,作PE∥CD,
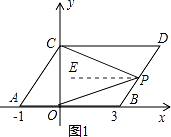
∵CD∥AB,
∴CD∥PE∥AB,
∴∠DCP=∠EPC,∠BOP=∠EPO,
∴∠DCP+∠BOP=∠EPC+∠EPO=∠CPO;
当点P在线段BD的延长线上时,如图2,作PE∥CD,
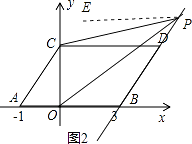
∵CD∥AB,
∴CD∥PE∥AB,
∴∠DCP=∠EPC,∠BOP=∠EPO,
∴∠EPO﹣∠EPC=∠BOP﹣∠DCP,
∴∠BOP﹣∠DCP=∠CPO;
同理可得当点P在线段DB的延长线上时,∠DCP﹣∠BOP=∠CPO.
【解析】(1)根据点的平移与坐标变换规律易得点C,D的坐标;
(2)先计算出S平行四边形ABOC=8,设M坐标为(0,m),根据三角形面积公式得![]() ×4×|m|=8,解得m=±4,于是可得M点的坐标为(0,4)或(0,-4);
×4×|m|=8,解得m=±4,于是可得M点的坐标为(0,4)或(0,-4);
(3)①先计算出S梯形OCDB=7,再讨论:当点P运动到点B时,S△BOC的最小值=3,则可判断S△CDP+S△BOP<4,当点P运动到点D时,S△BOC的最大值=4,于是可判断S△CDP+S△BOP>3,所以3<S△CDP+S△BOP<4;②分类讨论:当点P在BD上,如图1,作PE∥CD,根据平行线的性质得CD∥PE∥AB,则∠DCP=∠EPC,∠BOP=∠EPO,易得∠DCP+∠BOP=∠EPC+∠EPO=∠CPO;当点P在线段BD的延长线上时,如图2,同样有∠DCP=∠EPC,∠BOP=∠EPO,由于∠EPO-∠EPC=∠BOP-∠DCP,于是∠BOP-∠DCP=∠CPO;同理可得当点P在线段DB的延长线上时,∠DCP-∠BOP=∠CPO.
【考点精析】关于本题考查的三角形的面积,需要了解三角形的面积=1/2×底×高才能得出正确答案.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小伟遇到这样一个问题:如图1,在△ABC(其中∠BAC是一个可以变化的角)中,AB=2,AC=4,以BC为边在BC的下方作等边△PBC,求AP的最大值.
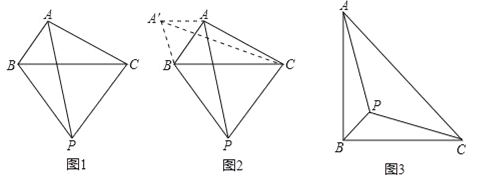
小伟是这样思考的:利用变换和等边三角形将边的位置重新组合.他的方法是以点B为旋转中心将△ABP逆时针旋转60°得到△A′BC,连接A′A,当点A落在A′C上时,此题可解(如图2).
(1)请你回答:AP的最大值是 .
(2)参考小伟同学思考问题的方法,解决下列问题:
如图3,等腰Rt△ABC.边AB=4,P为△ABC内部一点,请写出求AP+BP+CP的最小值长的解题思路.
提示:要解决AP+BP+CP的最小值问题,可仿照题目给出的做法.把△ABP绕B点逆时针旋转60,得到△A′BP′.
①请画出旋转后的图形
②请写出求AP+BP+CP的最小值的解题思路(结果可以不化简).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于N,连接MN,DN.请你判定四边形BMDN是什么特殊四边形,并说明理由. 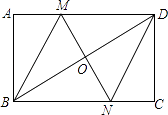
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.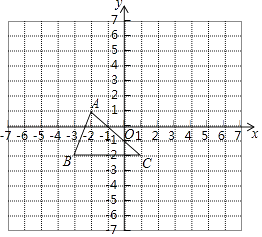
(1)在图中画出△A′B′C′;
(2)写出A′,B′的坐标;
(3)求三角形ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学小组的同学为了解“阅读经典”活动的开展情况,随机调查了50名同学,对他们一周的阅读时间进行了统计,并绘制成如图所示的条形统计图,这组数据的中位数和众数分别是( )
A.中位数和众数都是8小时
B.中位数是25人,众数是20人
C.中位数是13人,众数是20人
D.中位数是6小时,众数是8小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,AD+EC=AB. 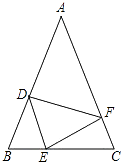
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com