
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于N,连接MN,DN.请你判定四边形BMDN是什么特殊四边形,并说明理由. 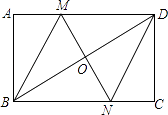
【答案】解:四边形BMDN是菱形.理由如下: ∵四边形ABCD是矩形,
∴AD∥BC,OD=OB,
∴∠MDO=∠NBO,
∵MN是BD的垂直平分线
∴在△MOD与△NOB中,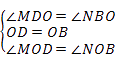 ,
,
∴△MOD≌△NOB(ASA),
∴MO=NO,
∴四边形BMDN是平行四边形.
∵MN是BD的垂直平分线,
∴平行四边形BMDN是菱形.
【解析】根据全等三角形的判定定理ASA证得△MOD≌△NOB,则由全等三角形的对应边相等推知MO=NO,所以“对角线互相平分的四边形BMDN是平行四边形,然后由”对角线互相垂直平分的平行四边形是菱形“证得结论﹣﹣四边形BMDN是菱形. ∴∠MOD=∠NOB=90°.
【考点精析】根据题目的已知条件,利用菱形的判定方法和矩形的性质的相关知识可以得到问题的答案,需要掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形;矩形的四个角都是直角,矩形的对角线相等.


科目:初中数学 来源: 题型:
【题目】如图,已知AB=A1B,A1B1=A1B2 , A2B2=A2B3 , A3B3=A3B4 , …若∠A=70°,则∠An的度数为( ) 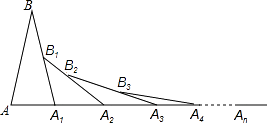
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=3,AB=5,D为AB边上一点,DE∥AC,交BC于点E,DF∥BC,交AC于点F,连接EF,则线段EF的最小值为 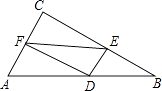
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2011次运动后,动点P的坐标是 . 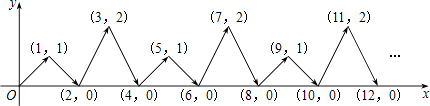
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年清明小长假期问,长春净月某景区接待游客约为51700人次,数字51700用科学记数法表示为( )
A.51.7×103B.5.17×104C.5.17×105D.0.517×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.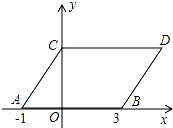
(1)求点C,D的坐标;
(2)若在y轴上存在点 M,连接MA,MB,使S△MAB=S平行四边形ABDC , 求出点M的坐标.
(3)若点P在直线BD上运动,连接PC,PO.
①若P在线段BD之间时(不与B,D重合),求S△CDP+S△BOP的取值范围;
②若P在直线BD上运动,请直接写出∠CPO、∠DCP、∠BOP的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com