
【题目】如图,Rt△ABC中,AB=AC=8,BO=![]() AB,点M为BC边上一动点,将线段OM绕点O按逆时针方向旋转90°至ON,连接AN、CN,则△CAN周长的最小值为________.
AB,点M为BC边上一动点,将线段OM绕点O按逆时针方向旋转90°至ON,连接AN、CN,则△CAN周长的最小值为________.

【答案】8+4![]() .
.
【解析】
过点O作OB′⊥AB于点O,交BC于点B′,连接B′N并延长交AB于点E,易证△BOM≌△B′ON(SAS),∴点N始终在经过点B′且与BC垂直的射线上,因为△CAN周长=CA+AN+CN=8+ AN+CN,所以AN+CN值最小时,周长最小,属于最短路径问题,关键找点C关于B′E的对称点C′,连接A C′,与B′E的交点N′即为周长最小时的点N,此时AN+CN=AC′,求出AC′的值即可求出周长最小值.
解:过点O作OB′⊥AB于点O,交BC于点B′,连接B′N并延长交AB于点E,∵Rt△ABC中,AB=AC,
∴∠OBB′=45°=∠OB′B,OB =OB′
又∵∠BOB′=∠MON=90°
∴∠BOM=∠B′ON
∴△BOM≌△B′ON(SAS)
∴∠OBB′=45°=∠OB′N,即∠BB′N=90°,OB′= OB=2,BB′=2![]() ,
,
∴点N始终在经过点B′且与BC垂直的射线上,
易证△BB′E是等腰直角三角形,BE=4,即BE=AE,
∵△CAN周长=CA+AN+CN=8+ AN+CN
∴AN+CN值最小时,周长最小,属于最短路径问题,
∴找点C关于B′E的对称点C′,连接A C′,与B′E的交点N′即为周长最小时的点N,此时AN+CN=AC′,
等腰直角三角形△BB′E中, 由勾股定理得BB′=2![]() ,
,
等腰直角三角形△ABC中, BC=8![]() 由三线合一得:BD=DC=AD=
由三线合一得:BD=DC=AD=![]() BC=4
BC=4![]() ,
,
∴B′C=BC- BB′=8![]() -2
-2![]() =6
=6![]() ,由对称性得:B′C=B′C′=6
,由对称性得:B′C=B′C′=6![]() ,
,
∴C′D=12![]() -4
-4![]() =8
=8![]() ,
,
即:Rt△AC′D中,A C′=![]() =
=![]() =4
=4![]()
∴△CAN周长的最小值=8+ AN+CN=8+4.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】图中的小方格都是边长为1的正方形,△ABC的顶点和O点都在正方形的顶点上.
(1)以点O为位似中心,在方格图中将△ABC放大为原来的2倍,得到△A′B′C′;
(2)△A′B′C′绕点B′顺时针旋转90°,画出旋转后得到的△A″B′C″,并求边A′B′在旋转过程中扫过的图形面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④△ABD边AB上的高等于DC.其中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④△ABD边AB上的高等于DC.其中正确的个数是( )

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在边长为4的菱形ABCD中,AC为其对角线,∠ABC=60°点M、N分别是边BC、边CD上的动点,且MB=NC.连接AM、AN、MN.MN交AC于点P.

(1)△AMN是什么特殊的三角形?说明理由.并求其面积最小值;
(2)求点P到直线CD距离的最大值;

(3)如图2,已知MB=NC=1,点E、F分别是边AM、边AN上的动点,连接EF、PF,EF+PF是否存在最小值?若存在,求出最小值及此时AE、AF的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC,BC=12厘米,点D为AB上一点且BD=8厘米,点P在线段BC上以2厘米/秒的速度由B点向C点运动,设运动时间为t,同时,点Q在线段CA上由C点向A点运动.

(1)用含t的式子表示PC的长为_______________;
(2)若点Q的运动速度与点p的运动速度相等,当t=2时,三角形BPD与三角形CQP是否全等,请说明理由;
(3)若点Q的运动速度与点P的运动速度不相等,请求出点Q的运动速度是多少时,能够使三角形BPD与三角形CQP全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,△ABC的顶点均在格点上,三个顶点的坐标分别是A(-3,4),B(-2,1),C(-4,2).
(1)将△ABC先向右平移7个单位长度,再向上平移2个单位长度,画出第二次平移后的△![]() ;
;
(2)以点O(0,0)为对称中心,画出与△ABC成中心对称的△![]() ;
;
(3)将点B绕坐标原点逆时针方向旋转90°至点![]() ,则点
,则点![]() 的坐标为(______,______)
的坐标为(______,______)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式![]() +(b﹣3)2=0,(c﹣4)2≤0
+(b﹣3)2=0,(c﹣4)2≤0
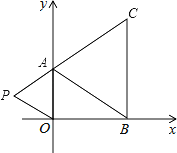
(1)求a、b、c的值;
(2)如果在第二象限内有一点P(﹣m,![]() ),请用含m的式子表示四边形ABOP的面积;
),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将四张边长各不相同的正方形纸片按如图方式放入矩形![]() 内(相邻纸片之间互不重叠也无缝隙),未被四张正方形纸片覆盖的部分用阴影表示.设右上角与左下角阴影部分的周长的差为
内(相邻纸片之间互不重叠也无缝隙),未被四张正方形纸片覆盖的部分用阴影表示.设右上角与左下角阴影部分的周长的差为![]() .若知道
.若知道![]() 的值,则不需测量就能知道周长的正方形的标号为( )
的值,则不需测量就能知道周长的正方形的标号为( )

A.①B.②C.③D.④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com