
【题目】如图1,在边长为4的菱形ABCD中,AC为其对角线,∠ABC=60°点M、N分别是边BC、边CD上的动点,且MB=NC.连接AM、AN、MN.MN交AC于点P.

(1)△AMN是什么特殊的三角形?说明理由.并求其面积最小值;
(2)求点P到直线CD距离的最大值;

(3)如图2,已知MB=NC=1,点E、F分别是边AM、边AN上的动点,连接EF、PF,EF+PF是否存在最小值?若存在,求出最小值及此时AE、AF的长;若不存在,请说明理由.
【答案】(1)△AMN为等边三角形,![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]()
【解析】
(1)△AMN是等边三角形,AM⊥BC时面积最小.只要证明△AMB≌△ANC,推出AM=AN,∠BAM=∠CAN即可解决问题.
(2)如图2中,当AM⊥BC时,点P到CD距离最大.作PE⊥CD于E.
(3)如图3中,作点P关于AN的对称点为K,过点K做AM的垂线,交AN为F,交AM为E,此时,EF+PF最短,连接AK、作AG⊥MN于G,MH⊥AB于H.首先求出AM、AG的长,再证明△AGP≌△KEA,推出KE=AG即可.
解:(1)△AMN为等边三角形;
如图1中,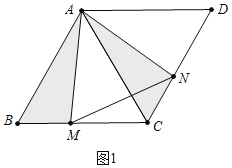
∵ABCD是菱形,∠ABC=60°,
∴△ABC为等边三角形
在△AMB和△ANC中,
AB=AC
∠B=∠ACN=60°
BM=NC
∴△AMB≌△ANC
∴AM=AN,∠BAM+∠MAC=∠MAC+∠NAC=60°,
∴∠MAN=60°,
∴△AMN为等边三角形,
当AM⊥BC时,△AMN的边长最小,面积最小,
此时AM=MN=AN=![]()
(2)如图2中,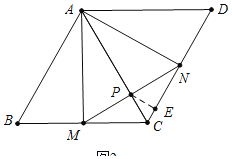
当AM⊥BC时,点P到CD距离最大.作PE⊥CD于E.
理由:由(1)可知△AMN是等边三角形,
当AM⊥BC时,△AMN的边长最小,此时PA长最小,PC的长最大,点P到直线CD距离的最大,
∵BM=MC=2,∠CMP=30°,∠MPC=90°,
∴PC=![]() MC=1,
MC=1,
在Rt△PCE中,∵∠CPE=30°,PC=1,
∴EC=![]() PC=
PC=![]() ,
,
∴PE=![]() .
.
∴点P到直线CD距离的最大值为![]() ;
;
(3)如图3中,作点P关于AN的对称点为K,过点K做AM的垂线,交AN为F,交AM为E,此时,EF+PF最短,由于对称,PF=KF,EF为垂线段(垂线段最短).
连接AK、作AG⊥MN于G,MH⊥AB于H.
在Rt△BMH中,∵BM=1,∠BMH=30°,
∴BH=![]() ,HM=
,HM=![]() ,
,
∴![]() ,
,
∵△AMN是等边三角形,
∴AG=![]() .
.
∵∠APG=∠PCM+∠PMC=60°+∠PMC,
∵∠PMC+∠PCM+∠CPM=180°,∠NAP+∠ANP+∠APN=180°,∠ANP=∠PCM=60°,∠APN=∠CPM,
∴∠CMP=∠NAP=∠NAK,
∵∠EAK=∠EAN+∠NAK=60°+∠NAK,
∴∠APG=∠EAK,
∵∠AGP=∠AEK=90°,AP=AK,
∴△AGP≌△KEA,
∴KE=AG=![]() .
.
∴EF+PF的最小值为![]() ,
,
∵∠PCN=∠PCM,
∴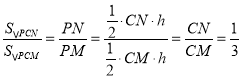 ,
,
∴PN=![]() ,
,
∴AE=PG=GN-PN=![]() ,
,
∵在Rt△AFE中,∠AFE=30°,∴AF=2AE,
∴AF=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知点A(﹣1,﹣2),点B(1,4)
(1)试建立相应的平面直角坐标系;
(2)描出线段AB的中点C,并写出其坐标;
(3)将线段AB沿水平方向向右平移3个单位长度得到线段A1B1,写出线段A1B1两个端点及线段中点C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书定价8元,如果一次购买10本以上,超过10本的部分打八折,在这个问题中,当购书的数量变化时,付款金额也随之发生了变化.
(1)如果购书的数量用x(本)表示,付款金额用y(元)表示,求y与x之间的关系式;
(2)当购书20本时,付款金额为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() 两地相距
两地相距![]() ,甲骑自行车,乙骑摩托车沿一条笔直的公路由
,甲骑自行车,乙骑摩托车沿一条笔直的公路由![]() 地匀速行驶到
地匀速行驶到![]() 地.设行驶时间为
地.设行驶时间为![]() ,甲、乙离开
,甲、乙离开![]() 地的路程分别记为
地的路程分别记为![]() ,
,![]() ,它们与
,它们与![]() 的关系如图所示.
的关系如图所示.

(1)分别求出线段![]() ,
,![]() 所在直线的函数表达式.
所在直线的函数表达式.
(2)试求点![]() 的坐标,并说明其实际意义.
的坐标,并说明其实际意义.
(3)乙在行驶过程中,求两人距离超过![]() 时
时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平价大药房准备购进![]() 、一次性医用两种口罩.两种口罩的进价和售价如表.已知:用
、一次性医用两种口罩.两种口罩的进价和售价如表.已知:用![]() 元购进一次性医用口罩的数量是用
元购进一次性医用口罩的数量是用![]() 元购进
元购进![]() 口罩的数量的
口罩的数量的![]() 倍.
倍.
| 一次性医用口罩 | |
进价(元 |
|
|
售价(元 |
|
|
(1)求![]() 的值;
的值;
(2)要使购进的![]() 、一次性医用两种口罩共
、一次性医用两种口罩共![]() 个的总利润不少于
个的总利润不少于![]() 元,且不超过
元,且不超过![]() 元,问该药店共有多少种进货方案?
元,问该药店共有多少种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,AB=AC=8,BO=![]() AB,点M为BC边上一动点,将线段OM绕点O按逆时针方向旋转90°至ON,连接AN、CN,则△CAN周长的最小值为________.
AB,点M为BC边上一动点,将线段OM绕点O按逆时针方向旋转90°至ON,连接AN、CN,则△CAN周长的最小值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.


(1)当直线MN绕点C旋转到图1的位置时,△ADC和△CEB全等吗?请说明理由.
(2)聪明的小亮发现,当直线MN绕点C旋转到图1的位置时,可得DE=AD+BE,请你说明其中的理由。
(3)小亮将直线MN绕点C旋转到图2的位置,线段DE、AD、BE之间存在着什么的数量关系,请写出这一关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿射线BC方向平移3 cm得到△DEF.若△ABC的周长为14 cm,则四边形ABFD的周长为( )

A. 20 cmB. 17 cm
C. 14 cmD. 23 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作体验:如图,在矩形ABCD中,点E、F分别在边AD、BC上,将矩形ABCD沿直线EF折叠,使点D恰好与点B重合,点C落在点C'处.点P为直线EF上一动点(不与E、F重合),过点P分别作直线BE、BF的垂线,垂足分别为点M和N,以PM、PN为邻边构造平行四边形PMQN.
(1)如图1,求证:BE=BF;
(2)特例感知:如图2,若DE=5,CF=3,当点P在线段EF上运动时,求平行四边形PMQN的周长;
(3)类比探究:如图3,当点P在线段EF的延长线上运动时,若DE=a,CF=b.请直接用含a、b的式子表示QM与QN之间的数量关系.(不要求写证明过程)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com