
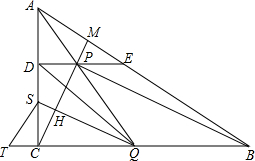
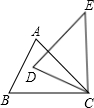
 ��ͼ��Rt��ABC�У���C=90�㣬D���E����AC��AB���ϣ���DE��BC��PΪ�߶�DE��һ�㣬ʹ�á�CPB=90�㣬CP���ӳ��߽�AB�ڵ�M���ӳ�AP��BC�ڵ�Q����Q��PB��ƽ���߽�PC�ڵ�H����AC�ڵ�S��TΪBC�ӳ�����һ�㣬������$\frac{MP}{CP}•\frac{BT}{CT}$=$\frac{PE}{DP}$+$\frac{PM}{CH}$������TS����֤��TS��DQ��
��ͼ��Rt��ABC�У���C=90�㣬D���E����AC��AB���ϣ���DE��BC��PΪ�߶�DE��һ�㣬ʹ�á�CPB=90�㣬CP���ӳ��߽�AB�ڵ�M���ӳ�AP��BC�ڵ�Q����Q��PB��ƽ���߽�PC�ڵ�H����AC�ڵ�S��TΪBC�ӳ�����һ�㣬������$\frac{MP}{CP}•\frac{BT}{CT}$=$\frac{PE}{DP}$+$\frac{PM}{CH}$������TS����֤��TS��DQ�� ���� ����Ҫ֤�Ľ��ۼ���DC��TQ��������֪��S�ǡ�DTQ�Ĵ��ģ�����ת��Ϊ֤��S�Ǵ��ļ��ɣ�Ҳ����ֻ��֤��QS��DT������������֪QS��CP���Ӷ�ֻ��Ҫ֤��CP��DT��ֻ��֤DPCT��ƽ���ı��Σ�ֻ��֤DP=CT��ֻ��֤$\frac{CT}{PE}=\frac{DP}{PE}$����$\frac{DP}{PE}=\frac{CQ}{BQ}=\frac{CH}{PH}$���Ӷ�ֻ��֤T��H��E���㹲���ɣ��ɴ˿��ǵ�÷�϶������涨����ֻ��֤$\frac{ME}{EB}•\frac{BT}{TC}•\frac{CH}{HM}=1$��Ҳ��ֻ��֤$\frac{ME}{EB}•\frac{BT}{TC}=\frac{HM}{CH}$��ֻ��֤$\frac{ME}{EB}•\frac{BT}{TC}=\frac{HP}{CH}+\frac{PM}{CH}$������QS��PB��DE��BC���������߶α�����ʽ����ʽ���ã�
��� ֤������ͼ������DT��ET��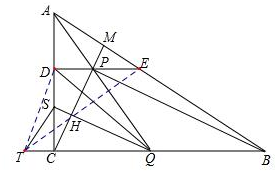
��DE��BC��
��$\frac{MP}{CP}=\frac{ME}{EB}$��$\frac{PE}{BQ}=\frac{AP}{AQ}=\frac{DP}{CQ}$��
��$\frac{PE}{DP}=\frac{BQ}{CQ}$��
��QS��PB��
��$\frac{BQ}{CQ}=\frac{HP}{CH}$��
��$\frac{PE}{DP}=\frac{HP}{CH}$��
��$\frac{MP}{CP}•\frac{BT}{CT}$=$\frac{PE}{DP}$+$\frac{PM}{CH}$��
��$\frac{ME}{EB}•\frac{BT}{TC}=\frac{HP}{CH}+\frac{PM}{CH}=\frac{HM}{CH}$��
��$\frac{ME}{EB}•\frac{BT}{TC}•\frac{CH}{HM}=1$��
��÷����˹�������涨����֪E��H��T���㹲�ߣ�
��$\frac{CT}{PE}=\frac{CH}{PH}=\frac{CQ}{BQ}=\frac{DP}{PE}$��
��CT=DP��
��CT��DP��
��TCPD��ƽ���ı��Σ�
��DT��CP��
��QS��PB��CP��PB��
��QS��DT��
��DC��TQ��
��S�ǡ�TDQ�Ĵ��ģ�
��TS��DQ��
֤�꣮
���� ���⿼��ƽ���߷��߶γɱ�����÷����˹�������涨���������εĴ������ʡ�ƽ���ı��ε��ж���֪ʶ�㣮���Ҫ֤�Ľ��۽�������̽������Ҫ�������DZ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ƽ��ֱ������ϵxOy�У�ֱ��y=2x+2��x�ᣬy��ֱ��ڵ�A��B��������y=ax2+bx-$\frac{2}{3}$������A�͵�C��4��0����
��ƽ��ֱ������ϵxOy�У�ֱ��y=2x+2��x�ᣬy��ֱ��ڵ�A��B��������y=ax2+bx-$\frac{2}{3}$������A�͵�C��4��0�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
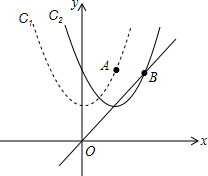 ��ͼ����֪������C1��y=$\frac{1}{2}$x2+2����һ��A����A�ĺ�����Ϊ2����������C1����ƽ�ƣ�ʹ�䶥������ֱ��y=x�ϣ���ʱ��������ΪC2����A�Ķ�Ӧ�����B��
��ͼ����֪������C1��y=$\frac{1}{2}$x2+2����һ��A����A�ĺ�����Ϊ2����������C1����ƽ�ƣ�ʹ�䶥������ֱ��y=x�ϣ���ʱ��������ΪC2����A�Ķ�Ӧ�����B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2a-b | B�� | -2a+b | C�� | -2a-b | D�� | a+2b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪AB=CD��AC=CE����Ҫʹ��ABC�ա�CDE������Ҫ���ӵ�һ�������ǡ�A=��DCE��
��ͼ����֪AB=CD��AC=CE����Ҫʹ��ABC�ա�CDE������Ҫ���ӵ�һ�������ǡ�A=��DCE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com