
【题目】在平面直角坐标系![]() 中,有抛物线
中,有抛物线![]() 和直线
和直线![]() 其中,直线与
其中,直线与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() .将点
.将点![]() 向右平移6个单位长度,得到点
向右平移6个单位长度,得到点![]() .
.
(1)求点![]() 的坐标和抛物线的对称轴;
的坐标和抛物线的对称轴;
(2)若抛物线与折线段![]() 恰有两个公共点,结合函数图象,求
恰有两个公共点,结合函数图象,求![]() 的取值范围.
的取值范围.
【答案】(1)C(6,6),对称轴为![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)先通过直线![]() 求得A、B坐标,再将点
求得A、B坐标,再将点![]() 向右平移6个单位长度,得到点
向右平移6个单位长度,得到点![]() 坐标,利用抛物线的对称轴公式求出对称轴即可;
坐标,利用抛物线的对称轴公式求出对称轴即可;
(2)先求出抛物线总会经过的两个定点(4,3),(-1,3),进而可求出抛物线与直线的一个交点坐标(-1,3),再分别讨论当m<0时,及当m>0时,需满足的条件即可.
(1)令![]() 中的y=0,则x=-2,
中的y=0,则x=-2,
令x=0,则y=6
∴A(-2,0),B(0,6),
∵将点![]() 向右平移6个单位长度,得到点
向右平移6个单位长度,得到点![]() .
.
∴C(6,6),
∵抛物线![]() ,
,
∴对称轴为![]()
(2)∵![]()
∴![]()
∴无论m为何值,抛物线总会经过定点(4,3),(-1,3),
又∵当x=-1时,直线y=-3+6=3,
∴直线也经过点(-1,3)
∴无论m为何值,抛物线与直线都总会经过(-1,3),
即(-1,3)为它们的一个交点坐标
当m<0时,如图,
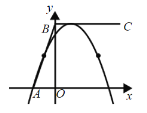
∵抛物线与折线段![]() 恰有两个公共点,
恰有两个公共点,
∴顶点一定在线段BC上,即顶点坐标为(![]() ,6)
,6)
将(![]() ,6)代入
,6)代入![]() 得
得![]() ,
,
此时![]()
令x=-2,则![]() >0,符合题意
>0,符合题意
∴![]() ;
;
当m>0时,如图,
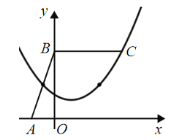
当抛物线经过点C(6,6)时
将(6,6)代入![]() 得
得![]() ,
,
∵抛物线与折线段![]() 恰有两个公共点,
恰有两个公共点,
且抛物线的开口越小,|m|的绝对值越大,
∴![]() .
.
综上所述,![]() 的取值范围为:
的取值范围为: ![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在□ABCD 中,对角线 AC 与 BD 相交于点 O ,点 E , F 分别为 OB , OD 的中点,延长 AE 至 G ,使 EG =AE ,连接 CG .
(1)求证: △ABE≌△CDF ;
(2)当 AB 与 AC 满足什么数量关系时,四边形 EGCF 是矩形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续的过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示.根据图象解答下列问题:

(1)洗衣机的进水时间是多少分钟?清洗时洗衣机中水量为多少升?
(2)已知洗衣机的排水速度为每分钟19升.
①求排水时洗衣机中的水量y(升)与时间x(分钟)与之间的关系式;
②如果排水时间为2分钟,求排水结束时洗衣机中剩下的水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
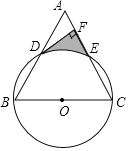
【题目】已知:如图,以等边△ABC的边BC为直径作⊙O,分别交AB,AC于点D,E,过点D作DF⊥AC交AC于点F.
(1)求证:DF是⊙O的切线;
(2)若等边△ABC的边长为8,求由![]() 、DF、EF围成的阴影部分面积.
、DF、EF围成的阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京世界园艺博览会(以下简称“世园会”)于2019年4月29日至10月7日在北京市延庆区举行.世园会为满足大家的游览需求,倾情打造了4条各具特色的游玩路线,如下表:
A | B | C | D |
漫步世园会 | 爱家乡,爱园艺 | 清新园艺之旅 | 车览之旅 |
小美和小红都计划去世园会游玩,她们各自在这4条路线中任意选择一条,每条线路被选择的可能性相同.
(1)求小美选择路线“清新园艺之旅”的概率是多少?
(2)用画树状图或列表的方法,求小美和小红恰好选择同一条路线的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将如图所示的牌面数字分别是1,2,3,4的四张扑克牌背面朝上,洗匀后放在桌面上.
(1)从中随机抽出一张牌,牌面数字是偶数的概率是__________;
(2)先从中随机抽出一张牌,将牌面数字作为十位上的数字(不放回),再随机抽取一张,将牌面数字作为个位上的数字,请用画树状图或列表的方法求组成的两位数恰好是3的倍数的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数,
为常数,![]() )的图象交于
)的图象交于![]() ,
,![]() 两点,
两点,![]() 点的坐标为(1,2).
点的坐标为(1,2).
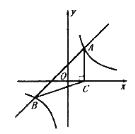
(1)求两个函数的表达式和![]() 点坐标;
点坐标;
(2)过点![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 轴于点
轴于点![]() ,求
,求![]() 的面积;
的面积;
(3)根据图象直接写出当![]() 时,自变量
时,自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 和四边形
和四边形![]() 都是平行四边形,点
都是平行四边形,点![]() 为
为![]() 的中点,
的中点,![]() 分别交
分别交![]() 于点
于点![]() ,平行四边形
,平行四边形![]() 的面积为 6,则图中阴影部分的面积为___________ .
的面积为 6,则图中阴影部分的面积为___________ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是![]() 元
元![]() 台经过市场销售后发现:在一个月内,当售价是
台经过市场销售后发现:在一个月内,当售价是![]() 元
元![]() 台时,可售出
台时,可售出![]() 台,且售价每降低
台,且售价每降低![]() 元,就可多售出
元,就可多售出![]() 台.若供货商规定这种空气净化器售价不能低于
台.若供货商规定这种空气净化器售价不能低于![]() 元
元![]() 台,代理销售商每月要完成不低于
台,代理销售商每月要完成不低于![]() 台的销售任务.
台的销售任务.
(1)试确定月销售量![]() (台)与售价
(台)与售价![]() (元
(元![]() 台)之间的函数关系式;
台)之间的函数关系式;
(2)求售价![]() 的范围;
的范围;
(3)当售价![]() (元
(元![]() 台)定为多少时,商场每月销售这种空气净化器所获得的利润
台)定为多少时,商场每月销售这种空气净化器所获得的利润![]() (元)最大?最大利润是多少?
(元)最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com