
【题目】在平面直角坐标系![]() 中,有一抛物线
中,有一抛物线![]() ,与
,与![]() 轴交于点
轴交于点![]() 、点
、点![]() ,现将背面完全相同,正面分别标有数
,现将背面完全相同,正面分别标有数![]() 、
、![]() 、
、![]() 、
、![]() 的
的![]() 张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数作为点
张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数作为点![]() 的横坐标,将该数的平方作为点
的横坐标,将该数的平方作为点![]() 的纵坐标,则点
的纵坐标,则点![]() 落在抛物线与
落在抛物线与![]() 轴围成的区域内(含边界)的概率为________.
轴围成的区域内(含边界)的概率为________.
【答案】![]()
【解析】
首先求出抛物线与坐标轴的交点,进而画出函数图象,再得出P坐标,进而判断P点位置求出概率.
当y=0,则0=-x2+2x+3,
解得:x1=-1,x2=3,
故抛物线与x轴交点为:(-1,0),(3,0),
当x=0,则y=3,则抛物线与y轴交点为:(0,3),
y=-x2+2x+3
=-(x-1)2+4,
故抛物线顶点坐标为:(1,4),
如图所示:
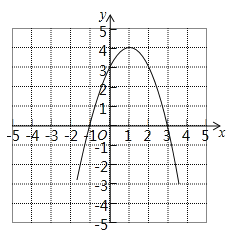
∵现将背面完全相同,正面分别标有数-1、0、1、2的4张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数作为点P的横坐标,将该数的平方作为点P的纵坐标,
∴P点坐标为:(-1,1),(0,0),(1,1),(2,4),
如图所示:(-1,1)一定不在抛物线与x轴围成的区域内;
(0,0),(1,1)一定在抛物线与x轴围成的区域内;
当x=2时,y=3,则(2,4)一定不在抛物线与x轴围成的区域内,
故点P落在抛物线与x轴围成的区域内(含边界)的概率为![]() .
.
故答案是:![]() .
.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】某中学为了提高学生的消防意识,举行了消防知识竞赛,所有参赛学生分别设有一、二、三等奖和纪念奖,获奖情况已绘制成如图所示的两幅不完整的统计图,根据图中所经信息解答下列问题:
(1)这次知识竞赛共有多少名学生?
(2)“二等奖”对应的扇形圆心角度数,并将条形统计图补充完整;
(3)小华参加了此次的知识竞赛,请你帮他求出获得“一等奖或二等奖”的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图四边形ABCD中,∠ABC=3∠CBD,∠ADC=3∠CDB,∠C=128°,则∠A的度数是( )
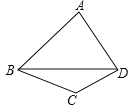
A.60°B.76°C.77°D.78°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 在
在![]() 的
的![]() 边上,
边上,![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,若添加条件________,则四边形
,若添加条件________,则四边形![]() 是矩形;若添加条件________,则四边形
是矩形;若添加条件________,则四边形![]() 是菱形;若添加条件________,则四边形
是菱形;若添加条件________,则四边形![]() 是正方形.
是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两地相距20千米,甲、乙两人都从A地去B地,图中l1和l2分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系,下列说法:①乙晚出发1小时;②乙出发3小时后追上甲;③甲的速度是4千米/时;④乙先到达B地.其中正确的是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长一定的正方形ABCD,Q是CD上一动点,AQ交BD于点M,过M作MN⊥AQ交BC于N点,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;
②MP=![]() BD;③BN+DQ=NQ;④
BD;③BN+DQ=NQ;④![]() 为定值。其中一定成立的是_______.
为定值。其中一定成立的是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B是数轴上两点,点A对应的数是-2,点B对应的数是2. △ABC是等边三角形,D是AB中点. 点M在AC边上,且AM=3CM.
(1)求CD长.
(2)点P是CD上的动点,确定点P使得PM+PA的值最小,并求出PM+PA的最小值.
(3)过点M的直线与数轴交于点Q,且QM![]() .点Q对应的数是t,结合图形直接写出t的取值范围.
.点Q对应的数是t,结合图形直接写出t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进甲、乙两种空调共50台.已知购进一台甲种空调比购进一台乙种空调进价少0.3万元;用20万元购进甲种空调数量是用40万元购进乙种空调数量的2倍.请解答下列问题:
(1)求甲、乙两种空调每台进价各是多少万元?
(2)若商场预计投入资金不少于10万元,且购进甲种空调至少31台,商场有哪几种购进方案?
(3)在(2)条件下,若甲种空调每台售价1100元,乙种空调每台售价4300元,甲、乙空调各有一台样机按八折出售,其余全部标价售出,商场从销售这50台空调获利中拿出2520元作为员工福利,其余利润恰好又可以购进以上空调共2台.请直接写出该商场购进这50台空调各几台.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com