练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】轮船从甲地顺水开往乙地，所用时间比从乙地逆水开往甲地少1.5小时。已知船在静水中的速度为18千米每小时，水流速度为2千米每小时，求甲乙两地之间的距离？

    【答案】甲乙两地之间的距离为120km.

    【解析】

    设轮船逆水航行从乙地到甲地需x小时，根据题意可得等量关系：顺水速度×顺水行驶时间=逆水速度×逆水行驶时间，根据等量关系列出方程，再解即可．

    解：设轮船逆水航行从乙地到甲地需x小时，
    根据题意，得（18+2）（x-1.5）=（18-2）x，
    解得：x=7.5，
    （18-2）×7.5=120．
    即：甲、乙两地之间的距离为120km．
    故答案是：120 km．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知光的速度为300 000 000米/秒，太阳光到达地球的时间大约是500秒，试计算太阳与地球的距离大约是千米．（结果用科学记数法表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知|a－3|＋(b+4)2=0，则(a+b)2003＝___．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在数轴上与表示﹣3的点的距离等于2的点所表示的数是（ ）
    A.1
    B.5
    C.1或﹣2
    D.﹣1或﹣5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某经销商销售一种产品，这种产品的成本价为10元／千克，市场调查发现，该产品每天的销售量y（千克）与销售价x(元／千克，且10≤x≤18)之间的函数关系如图所示：

    (1)求y(千克)与销售价z的函数关系式；

    (2)该经销商想要每天获得150元的销售利润，销售价应定为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，图1是一个长为2m，宽为2n的长方形，沿图中的虚线剪成四个全等的小长方形，再按图2围成一个较大的正方形．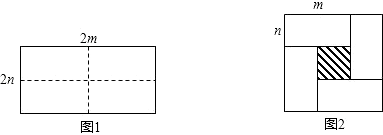

    （1）请用两种方法表示图2中阴影部分的面积（只需表示，不必化简）；
    （2）比较（1）的两种结果，你能得到怎样的等量关系？
    （3）请你用（2）中得到的等量关系解决下面问题：如果m﹣n=4，mn=12，求m+n的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一次函数y＝ax＋b交x轴于点(－5，0)，则关于x的方程ax＋b＝0的解是( )

    A. x＝5 B. x＝－5 C. x＝0 D. 无法求解

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】乘法公式的探究及应用．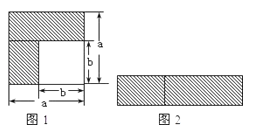

    （1）如图1，可以求出阴影部分的面积是 （写成两数平方差的形式）；
    （2）如图2，若将阴影部分裁剪下来，重新拼成一个矩形，它的宽是 ，长是 面积是 （写成多项式乘法的形式）；
    （3）比较图1、图2阴影部分的面积，可以得到公式 ；
    （4）运用你所得到的公式，计算下列各题：
    ①10.2×9.8，②（2m+n﹣p）（2m﹣n+p）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在正方形ABCD中，对角线AC，BD交于点O，点P在线段BC上（不含点B），∠BPE＝∠ACB，PE交BO于点E，过点B作BF⊥PE，垂足为F，交AC于点G．

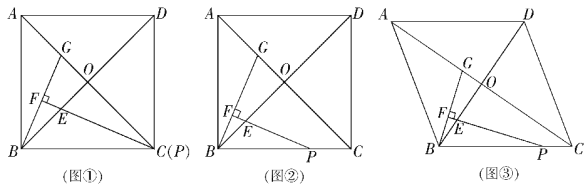
    （1） 当点P与点C重合时（如图①）．求证：△BOG≌△POE；（4分）

    （2）通过观察、测量、猜想：= ，并结合图②证明你的猜想；（5分）

    （3）把正方形ABCD改为菱形，其他条件不变（如图③），若∠ACB=α，求的值．（用含α的式子表示）（5分）

    查看答案和解析>>

    同步练习册答案