
【题目】已知四边形ABCD内接于⊙O,∠DAB=90°.
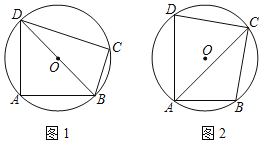
(Ⅰ)如图1,连接BD,若⊙O的半径为6,弧AD=弧AB,求AB的长;
(Ⅱ)如图2,连接AC,若AD=5,AB=3,对角线AC平分∠DAB,求AC的长.
【答案】(Ⅰ)6![]() ;(Ⅱ)4
;(Ⅱ)4![]()
【解析】
(Ⅰ)如图1,先利用圆周角定理得到BD为直径,即BD=12,再证明△ABD为等腰直角三角形,然后根据等腰直角三角形求出AB;
(Ⅱ)如图2,连接BD,作BH⊥AC于H,先利用圆周角定理得到BD为直径,利用勾股定理计算出BD=![]() ,再证明△CDB为等腰直角三角形得到BC=
,再证明△CDB为等腰直角三角形得到BC=![]() BD=
BD=![]() ,接着在Rt△ABH中计算出AH=BH=
,接着在Rt△ABH中计算出AH=BH=![]() ,然后在Rt△BCH中计算出CH=
,然后在Rt△BCH中计算出CH=![]() ,从而得到AC的长.
,从而得到AC的长.
解:(Ⅰ)如图1,
∵∠DAB=90°,
∴BD为直径,即BD=12,
∵![]() ,
,
∴AD=AB,
∴△ABD为等腰直角三角形,
∴AB=![]() BD=6
BD=6![]() ;
;
(Ⅱ)如图2,连接BD,作BH⊥AC于H,
∵∠DAB=90°,
∴BD为直径,BD=![]() =
=![]() ,
,
∴∠BCD=90°,
∵AC平分∠DAB,
∴∠BAC=∠BAC=45°,
∴∠CBD=∠BDC=45°,
∴△CDB为等腰直角三角形,
∴BC=![]() BD=
BD=![]() ×
×![]() =
=![]() ,
,
在Rt△ABH中,AH=BH=![]() AB=
AB=![]() ,
,
在Rt△BCH中,CH=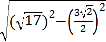 =
=![]() ,
,
∴AC=AH+CH=![]() =4
=4![]() .
.



 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】某学校自主开发了A书法、B阅读,C绘画,D器乐四门选修课程供学生选择,每门课程被选到的机会均等.
(1)若学生小玲计划选修两门课程,请写出她所有可能的选法;
(2)若学生小强和小明各计划选修一门课程,则他们两人恰好选修同一门课程的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在宣传“民族团结”活动中,采用四种宣传形式:A.器乐,B.舞蹈,C.朗诵,D.唱歌.每名学生从中选择并且只能选择一种最喜欢的,学校就宣传形式对学生进行了抽样调查,并将调查结果绘制了如下两幅不完整的统计图:
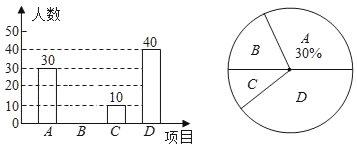
请结合图中所给信息,解答下列问题
(1)本次调查的学生共有 人;
(2)补全条形统计图;
(3)七年级一班在最喜欢“器乐”的学生中,有甲、乙、丙、丁四位同学表现优秀,现从这四位同学中随机选出两名同学参加学校的器乐队,请用列表或画树状图法求被选取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元.市场调査发现,若每箱以50元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天销售量![]() (箱)与销售价
(箱)与销售价![]() (元/箱)之间的函数关系式.
(元/箱)之间的函数关系式.
(2)求该批发商平均每天的销售利润![]() (元)与销售价
(元)与销售价![]() (元/箱)之间的函数关系式.
(元/箱)之间的函数关系式.
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)求证:BC2=2CDOE;
(3)若![]() ,求OE的长.
,求OE的长.
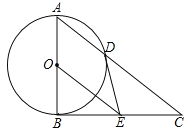
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“早黑宝”葡萄品种是我省农科院研制的优质新品种,在我省被广泛种植,邓州市某葡萄种植基地2017年种植“早黑宝”100亩,到2019年“卓黑宝”的种植面积达到196亩.
(1)求该基地这两年“早黑宝”种植面积的平均增长率;
(2)市场调查发现,当“早黑宝”的售价为20元/千克时,每天能售出200千克,售价每降价1元,每天可多售出50千克,为了推广宣传,基地决定降价促销,同时减少库存,已知该基地“早黑宝”的平均成本价为12元/千克,若使销售“早黑宝”每天获利1750元,则售价应降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有若千间标准客房,当房价为200元/间时,日均入住数为60间.市场调查表明,在物价局核定的每间标准房价格在160~220元之间(含160元,220元)浮动时,每提高10元,日均入住数减少10间.在不考虑其他因素的前提下,设标准房的价格为x元/间,日均入住数为y间. .
(1) y关于x的解析式为_ .
(2)当标准房的价格定为多少元时,客房的日营业额为10500元?
(3)当标准房的价格定为多少元时,客房的日营业额最大,最大为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克30元,规定每千克售价不低于成本,且不高于70元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 40 | 50 | 60 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入成本);
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com