Question

【题目】如图，在平面直角坐标系中，边长为1的正方形OA1B1C1的两边在坐标轴上，以它的对角线OB1为边作正方形OB1B2C2 ， 再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3 ， 以此类推…则正方形OB2016B2017C2017的顶点B2017的坐标是（ ）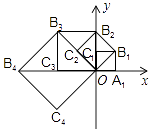

A.（21008 ， 0）
B.（21008 ， 21008）
C.（0，21008）
D.（21007 ， 21007）

Answer 1

【答案】B
【解析】观察，发现：B1（1，1），B2（0，2），B3（﹣2，2），B4（﹣4，0），B5（﹣4，﹣4），B6（0，﹣8），B7（8，﹣8），B8（16，0），B9（16，16），…，

∴B8n+1（24n，24n）（n为自然数）．

∵2017=8×252+1，

∴点B2017的坐标为（21008，21008）．

所以答案是：B．

【考点精析】本题主要考查了正方形的性质的相关知识点，需要掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题．