【题目】如图，一次函数y＝kx+b的图象分别交x轴，y轴于A（4.0），B（0，2）两点，与反比例函数y＝
的图象交于C．D两点，CE⊥x轴于点E且CE＝3．
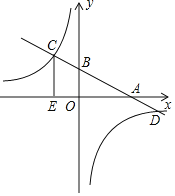
（1）求反比例函数与一次函数的解析式；
（2）根据图象直接写出：不等式0＜kx+b＜的解集．
【答案】（1）y＝﹣
+2，y＝﹣
；（2）﹣2＜x＜0
【解析】
（1）根据待定系数法即可求得一次函数的解析式，由题意可知C的纵坐标为3，代入一次函数解析式即可求得C的坐标，然后代入y=
求得m的值，即可求得反比例函数的解析式；
（2）根据图象找出y＝kx+b在x轴上方且在y=的下方的图象对应的x的范围．
（1）根据题意，得
，
解得k＝﹣
，b＝2，
所以一次函数的解析式为y＝﹣+2，
由题意可知，点C的纵坐标为3．
把y＝3代入y＝﹣+2，中，得x＝﹣2．
所以点C坐标为（﹣2，3）．
把点C坐标（﹣2，3）代入y＝中，
解得m＝﹣6．
所以反比例函数的解析式为y＝﹣；
（2）根据图像可得：不等式0＜kx+b＜的解集是：﹣2＜x＜0．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
目标测试系列答案科目：初中数学 来源： 题型：
【题目】某区域平面示意图如图，点O在河的一侧，AC和BC表示两条互相垂直的公路．甲勘测员在A处测得点O位于北偏东45°，乙勘测员在B处测得点O位于南偏西73.7°，测得AC=840m，BC=500m．请求出点O到BC的距离．参考数据：sin73.7°≈
，cos73.7°≈
，tan73.7°≈
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我县为积极响应创建“省级卫生城市”的号召，为打造“绿色乐至，健康乐至”是我们每个乐至人应尽的义务.某乡镇积极开展垃圾分类有效回收，据统计2017年有效回收的垃圾约1.5万吨，截止2019年底，有效回收的垃圾约2.8万吨，设这两年该乡镇的垃圾有效回收平均增长率为x，则下列方程正确的是（ ）.
A.1.5（1+2x）＝2.8B.
C.
D.
+
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若二次函数
的图象与
轴分别交于点
、
，且过点
.
（1）求二次函数表达式；
（2）若点
为抛物线上第一象限内的点，且
,求点的坐标；
（3）在抛物线上（
下方）是否存在点
，使
？若存在，求出点到
轴的距离；若不存在，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题情境:在综合实践课上，老师让同学们以“菱形纸片的剪拼”为主题开展数学活动，如图（1），将一张菱形纸片ABCD（∠BAD＝60°）沿对角线AC剪开，得到△ABC和△ACD
操作发现:（1）将图（1）中的△ABC以A为旋转中心，顺时针方向旋转角α（0°＜α＜60°）得到如图（2）所示△ABC′，分别延长BC′和DC交于点E，发现CE＝C′E．请你证明这个结论．
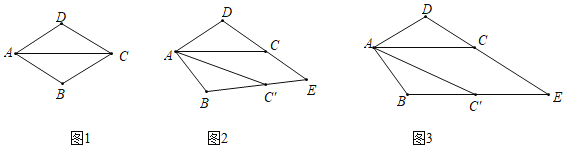
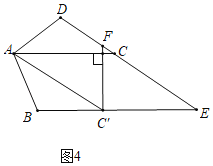
（2）在问题（1）的基础上，当旋转角α等于多少度时，四边形ACEC′是菱形？请你利用图（3）说明理由．
拓展探究:（3）在满足问题（2）的基础上，过点C′作C′F⊥AC，与DC交于点F．试判断AD、DF与AC的数量关系，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在一张矩形纸片ABCD中，AB=4，BC=8，点E，F分别在AD，BC上，将纸片ABCD沿直线EF折叠，点C落在AD上的一点H处，点D落在点G处，有以下四个结论：
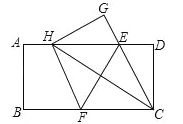
①四边形CFHE是菱形；
②EC平分∠DCH；
③线段BF的取值范围为3≤BF≤4；
④当点H与点A重合时，EF=2
．
以上结论中，你认为正确的有 ．（填序号）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一次函数
分别与
轴、
轴交于点
、
.顶点为
的抛物线经过点.
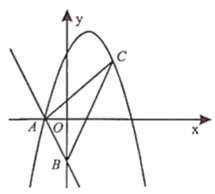
（1）求抛物线的解析式；
（2）点
为第一象限抛物线上一动点.设点的横坐标为
，
的面积为
.当为何值时，的值最大，并求的最大值；
（3）在（2）的结论下，若点
在轴上，
为直角三角形，请直接写出点的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
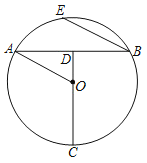
【题目】如图，已知AB是⊙O的弦，点C在⊙O上，且
，联结AO，CO，并延长CO交弦AB于点D，AB＝4
，CD＝6．
（1）求∠OAB的大小；
（2）若点E在⊙O上，BE∥AO，求BE的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
