
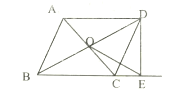
【题目】如图,平行四边形![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,点
,点![]() 是边
是边![]() 的延长线上一点,且
的延长线上一点,且![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)如果![]() ,求证:
,求证:![]() .
.
【答案】(1)见解析;(2)见解析.
【解析】
(1)由平行四边形的性质得到BO=OD,由等量代换推出OE=OD,根据平行四边形的判定即可得到结论;
(2)根据等角的余角相等,得到∠CEO=∠CDE,从而可证∠DBE=∠CDE,推出△BDE∽△CDE,即可得到结论.
证明:(1)∵四边形ABCD是平行四边形,
∴BO=OD,
∵OE=OB,
∴OE=OD,
∴∠OBE=∠OEB,∠OED=∠ODE,
∵∠OBE+∠OEB+∠OED+∠ODE=180°,
∴∠BEO+∠DEO=∠BED=90°,
∴DE⊥BE;
(2)∵OE⊥CD∴∠CEO+∠DCE=∠CDE+∠DCE=90°,
∴∠CEO=∠CDE,
∵OB=OE,
∴∠DBE=∠CDE,
∵∠BED=∠BED,
∴△BDE∽△DCE,
∴![]() ,
,
∵BD=2OB=2OE,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,P是直径AB上的一点,AB=6,CP⊥AB交半圆![]() 于点C,以BC为直角边构造等腰Rt△BCD,∠BCD=90°,连接OD.
于点C,以BC为直角边构造等腰Rt△BCD,∠BCD=90°,连接OD.

小明根据学习函数的经验,对线段AP,BC,OD的长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)对于点P在AB上的不同位置,画图、测量,得到了线段AP,BC,OD的长度的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置… | |
AP | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | … |
BC | 6.00 | 5.48 | 4.90 | 4.24 | 3.46 | 2.45 | … |
OD | 6.71 | 7.24 | 7.07 | 6.71 | 6.16 | 5.33 | … |
在AP,BC,OD的长度这三个量中,确定________的长度是自变量,________的长度和________的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;

(3)结合函数图象,解决问题:当OD=2BC时,线段AP的长度约为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里,装有若干个完全相同的A、B、C三种球,其中A球x个,B球x个,C球(x+1)个.若从中任意摸出一个球是A球的概率为0.25.
(1)这个袋中A、B、C三种球各多少个?
(2)若小明从口袋中随机模出1个球后不放回,再随机摸出1个.请你用画树状图的方法求小明摸到1个A球和1个C球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
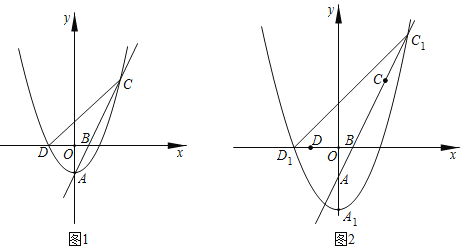
【题目】如图1,抛物线W:y=ax2﹣2的顶点为点A,与x轴的负半轴交于点D,直线AB交抛物线W于另一点C,点B的坐标为(1,0).
(1)求直线AB的解析式;
(2)过点C作CE⊥x轴,交x轴于点E,若AC平分∠DCE,求抛物线W的解析式;
(3)若a=![]() ,将抛物线W向下平移m(m>0)个单位得到抛物线W1,如图2,记抛物线W1的顶点为A1,与x轴负半轴的交点为D1,与射线BC的交点为C1.问:在平移的过程中,tan∠D1C1B是否恒为定值?若是,请求出tan∠D1C1B的值;若不是,请说明理由.
,将抛物线W向下平移m(m>0)个单位得到抛物线W1,如图2,记抛物线W1的顶点为A1,与x轴负半轴的交点为D1,与射线BC的交点为C1.问:在平移的过程中,tan∠D1C1B是否恒为定值?若是,请求出tan∠D1C1B的值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“网购”的增多,快递业务发展迅速。我市某快递公司今年八月份与十月份完成投递的快递总件数分别为![]() 万件和
万件和![]() 万件,假定该公司每月的投递总件数的增长率相同.
万件,假定该公司每月的投递总件数的增长率相同.
(1)求该快递公司每月的投递总件数的月平均增长率;
(2)由于“双十一”购买量激增,预计11月需投递的快递总件数的增长率将是原来![]() 倍,如果每人每月最多可投递快递
倍,如果每人每月最多可投递快递![]() 万件,该公司现有
万件,该公司现有![]() 名业务员,是否能完成当月投递任务?如果不能,需临时招聘几名业务员?
名业务员,是否能完成当月投递任务?如果不能,需临时招聘几名业务员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0)和B点,与y轴交于点C(0,﹣3).
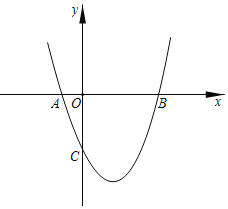
(1)求该抛物线的解析式;
(2)观察图象,直接写出不等式x2+bx+c>0的解集;
(3)设(1)中的抛物线上有一个动点P,点P在该抛物线上滑动且满足S△PAB=8,请求出此时P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程ax2+bx+1=0中,b=![]() ;
;
(1)若a=4,求b的值;
(2)若方程ax2+bx+1=0有两个相等的实数根,求方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,台风中心位于点![]() ,并沿东北方向
,并沿东北方向![]() 移动,已知台风移动的速度为40千米/时,受影响区域的半径为260千米,
移动,已知台风移动的速度为40千米/时,受影响区域的半径为260千米,![]() 市位于点
市位于点![]() 的北偏东75°方向上,距离
的北偏东75°方向上,距离![]() 点480千米.
点480千米.

(1)说明本次台风是否会影响![]() 市;
市;
(2)若这次台风会影响![]() 市,求
市,求![]() 市受台风影响的时间.
市受台风影响的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程ax2+bx+1=0中,b=![]() ;
;
(1)若a=4,求b的值;
(2)若方程ax2+bx+1=0有两个相等的实数根,求方程的根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com