
”¾ĢāÄæ”æĖę×Å”°Ķų¹ŗ”±µÄŌö¶ą£¬æģµŻŅµĪń·¢Õ¹ŃøĖŁ”£ĪŅŹŠÄ³æģµŻ¹«Ė¾½ńÄź°ĖŌĀ·ŻÓėŹ®ŌĀ·ŻĶź³ÉĶ¶µŻµÄæģµŻ×ܼžŹż·Ö±šĪŖ![]() Ķņ¼žŗĶ
Ķņ¼žŗĶ![]() Ķņ¼ž£¬¼Ł¶ØøĆ¹«Ė¾ĆæŌĀµÄĶ¶µŻ×ܼžŹżµÄŌö³¤ĀŹĻąĶ¬.
Ķņ¼ž£¬¼Ł¶ØøĆ¹«Ė¾ĆæŌĀµÄĶ¶µŻ×ܼžŹżµÄŌö³¤ĀŹĻąĶ¬.
£Ø1£©ĒóøĆæģµŻ¹«Ė¾ĆæŌĀµÄĶ¶µŻ×ܼžŹżµÄŌĀĘ½¾łŌö³¤ĀŹ£»
£Ø2£©ÓÉÓŚ”°Ė«Ź®Ņ»”±¹ŗĀņĮ漤Ōö£¬Ō¤¼Ę11ŌĀŠčĶ¶µŻµÄæģµŻ×ܼžŹżµÄŌö³¤ĀŹ½«ŹĒŌĄ“![]() ±¶£¬Čē¹ūĆæČĖĆæŌĀ×ī¶ąæÉĶ¶µŻæģµŻ
±¶£¬Čē¹ūĆæČĖĆæŌĀ×ī¶ąæÉĶ¶µŻæģµŻ![]() Ķņ¼ž£¬øĆ¹«Ė¾ĻÖÓŠ
Ķņ¼ž£¬øĆ¹«Ė¾ĻÖÓŠ![]() ĆūŅµĪńŌ±£¬ŹĒ·ńÄÜĶź³Éµ±ŌĀĶ¶µŻČĪĪń£æČē¹ū²»ÄÜ£¬ŠčĮŁŹ±ÕŠĘø¼øĆūŅµĪńŌ±£æ
ĆūŅµĪńŌ±£¬ŹĒ·ńÄÜĶź³Éµ±ŌĀĶ¶µŻČĪĪń£æČē¹ū²»ÄÜ£¬ŠčĮŁŹ±ÕŠĘø¼øĆūŅµĪńŌ±£æ
”¾“š°ø”æ£Ø1£©![]() £»£Ø2£©øĆ¹«Ė¾ĻÖÓŠ
£»£Ø2£©øĆ¹«Ė¾ĻÖÓŠ![]() ĆūŅµĪńŌ±£¬²»ÄÜĶź³ÉŌĀĶ¶µŻČĪĪń£¬ŠčĮŁŹ±ÕŠĘø
ĆūŅµĪńŌ±£¬²»ÄÜĶź³ÉŌĀĶ¶µŻČĪĪń£¬ŠčĮŁŹ±ÕŠĘø![]() ĆūŅµĪńŌ±.
ĆūŅµĪńŌ±.
”¾½āĪö”æ
£Ø1£©ÉčøĆæģµŻ¹«Ė¾Ķ¶µŻ×ܼžŹżµÄŌĀĘ½¾łŌö³¤ĀŹĪŖx£¬øł¾Ż”°½ńğȿŌĀ·ŻÓėĪåŌĀ·ŻĶź³ÉĶ¶µŻµÄæģµŻ×ܼžŹż·Ö±šĪŖ10Ķņ¼žŗĶ12.1Ķņ¼ž£¬ĻÖ¼Ł¶ØøĆ¹«Ė¾ĆæŌĀĶ¶µŻµÄæģµŻ×ܼžŹżµÄŌö³¤ĀŹĻąĶ¬”±½ØĮ¢·½³Ģ£¬½ā·½³Ģ¼“æÉ£»
£Ø2£©Ź×ĻČĒó³ö½ńÄź11ŌĀ·ŻµÄæģµŻĶ¶µŻČĪĪń£¬ŌŁĒó³ö21ĆūæģµŻĶ¶µŻŅµĪńŌ±ÄÜĶź³ÉµÄæģµŻĶ¶µŻČĪĪń£¬±Č½ĻµĆ³öøĆ¹«Ė¾²»ÄÜĶź³É½ńÄź6ŌĀ·ŻµÄæģµŻĶ¶µŻČĪĪń£®
½ā£ŗ£Ø1£©ÉčøĆæģµŻ¹«Ė¾ĆæŌĀµÄĶ¶µŻ×ܼžŹżµÄŌĀĘ½¾łŌö³¤ĀŹĪŖ![]()
ÓÉĢāŅāµĆ£¬ ![]()
½āµĆ![]() £¬
£¬![]() £ØÉį£©
£ØÉį£©
ÉčøĆæģµŻ¹«Ė¾ĆæŌĀµÄĶ¶µŻ×ܼžŹżµÄŌĀĘ½¾łŌö³¤ĀŹĪŖ![]() ”£
ӣ
£Ø2£©½ńÄź11ŌĀ·ŻµÄæģµŻĶ¶µŻČĪĪńŹĒ12.1”Į£Ø1+10%£©=13.31£ØĶņ¼ž£©£®
”ßĘ½¾łĆæČĖĆæŌĀ×ī¶ąæÉĶ¶µŻ0.6Ķņ¼ž£¬
”ą21ĆūæģµŻĶ¶µŻŅµĪńŌ±ÄÜĶź³ÉµÄæģµŻĶ¶µŻČĪĪńŹĒ£ŗ0.6”Į21=12.6£¼13.31£¬
”ąøĆ¹«Ė¾ĻÖÓŠµÄ21ĆūæģµŻĶ¶µŻŅµĪńŌ±²»ÄÜĶź³É½ńÄź11ŌĀ·ŻµÄæģµŻĶ¶µŻČĪĪń£®
ÖĮÉŁŅŖŌö¼Ó2ĆūŅµĪńŌ±£®


 °ŁÄźŃ§µäæĪŹ±Ń§Į·²āĻµĮŠ“š°ø
°ŁÄźŃ§µäæĪŹ±Ń§Į·²āĻµĮŠ“š°ø ČŹ°®Ó¢ÓļĶ¬²½Į·Ļ°²įĻµĮŠ“š°ø
ČŹ°®Ó¢ÓļĶ¬²½Į·Ļ°²įĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”ŃOÖŠ£¬°ė¾¶OC=6£¬DŹĒ°ė¾¶OCÉĻŅ»µć£¬ĒŅ OD=4£®A£¬BŹĒ”ŃOÉĻµÄĮ½øö¶Æµć£¬”ĻADB=90”ć£¬FŹĒABµÄÖŠµć£¬ŌņOFµÄ³¤µÄ×ī“óÖµµČÓŚ______£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬¹ż”ŃTĶāŅ»µćPŅżĖüµÄĮ½ĢõĒŠĻߣ¬ĒŠµć·Ö±šĪŖM£¬N£¬Čō![]() £¬Ōņ³ĘPĪŖ”ŃTµÄ»·ČĘµć£®
£¬Ōņ³ĘPĪŖ”ŃTµÄ»·ČĘµć£®
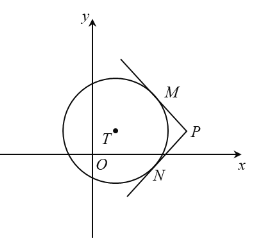
(1)µ±”ŃO°ė¾¶ĪŖ1Ź±£¬
¢ŁŌŚ![]() ÖŠ£¬”ŃOµÄ»·ČʵćŹĒ_________;
ÖŠ£¬”ŃOµÄ»·ČʵćŹĒ_________;
¢ŚÖ±Ļßy=2x+bÓėxÖį½»ÓŚµćA£¬yÖį½»ÓŚµćB£¬ČōĻ߶ĪABÉĻ“ęŌŚ”ŃOµÄ»·ČĘµć£¬ĒóbµÄȔֵ·¶Ī§£»
(2)”ŃTµÄ°ė¾¶ĪŖ1£¬Ō²ŠÄĪŖ£Ø0£¬t£©£¬ŅŌ![]() ĪŖŌ²ŠÄ£¬
ĪŖŌ²ŠÄ£¬![]() ĪŖ°ė¾¶µÄĖłÓŠŌ²¹¹³ÉĶ¼ŠĪH£¬ČōŌŚĶ¼ŠĪHÉĻ“ęŌŚ”ŃTµÄ»·ČĘµć£¬Ö±½ÓŠ“³ötµÄȔֵ·¶Ī§.
ĪŖ°ė¾¶µÄĖłÓŠŌ²¹¹³ÉĶ¼ŠĪH£¬ČōŌŚĶ¼ŠĪHÉĻ“ęŌŚ”ŃTµÄ»·ČĘµć£¬Ö±½ÓŠ“³ötµÄȔֵ·¶Ī§.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
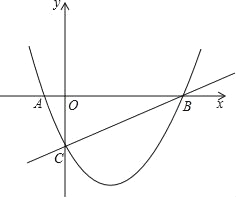
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖÅ×ĪļĻßy=ax2©![]() x+cÓėxÖįĻą½»ÓŚA”¢BĮ½µć£¬²¢ÓėÖ±Ļßy=
x+cÓėxÖįĻą½»ÓŚA”¢BĮ½µć£¬²¢ÓėÖ±Ļßy=![]() x©2½»ÓŚB”¢CĮ½µć£¬ĘäÖŠµćCŹĒÖ±Ļßy=
x©2½»ÓŚB”¢CĮ½µć£¬ĘäÖŠµćCŹĒÖ±Ļßy=![]() x©2ÓėyÖįµÄ½»µć£¬Į¬½ÓAC£®
x©2ÓėyÖįµÄ½»µć£¬Į¬½ÓAC£®
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©Ö¤Ć÷£ŗ”÷ABCĪŖÖ±½ĒČż½ĒŠĪ£»
£Ø3£©”÷ABCÄŚ²æÄÜ·ń½Ų³öĆ껿×ī“óµÄ¾ŲŠĪDEFG£æ£Ø¶„µćD”¢E”¢F”¢GŌŚ”÷ABCø÷±ßÉĻ£©ČōÄÜ£¬Ēó³ö×ī“óĆ껿£»Čō²»ÄÜ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
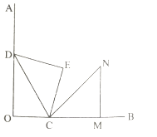
”¾ĢāÄæ”æČēĶ¼![]() £¬
£¬![]() ŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬µć
ŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬µć![]() ”¢
”¢![]() ·Ö±šŌŚ
·Ö±šŌŚ![]() ”¢
”¢![]() ÉĻ£¬
ÉĻ£¬![]() £¬½«
£¬½«![]() Čʵć
Čʵć![]() Ė³Ź±ÕėŠż×Ŗ
Ė³Ź±ÕėŠż×Ŗ![]() £¬µć
£¬µć![]() µÄ¶ŌÓ¦µć
µÄ¶ŌÓ¦µć![]() Ē”ŗĆĀäŌŚ
Ē”ŗĆĀäŌŚ![]() ÉĻ£¬Ōņ
ÉĻ£¬Ōņ![]() ÖµĪŖ£Ø£©
ÖµĪŖ£Ø£©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ę½ŠŠĖıߊĪ![]() µÄ¶Ō½ĒĻß
µÄ¶Ō½ĒĻß![]() ”¢
”¢![]() Ļą½»ÓŚµć
Ļą½»ÓŚµć![]() £¬µć
£¬µć![]() ŹĒ±ß
ŹĒ±ß![]() µÄŃÓ³¤ĻßÉĻŅ»µć£¬ĒŅ
µÄŃÓ³¤ĻßÉĻŅ»µć£¬ĒŅ![]() £¬Į¬½Ó
£¬Į¬½Ó![]() .
.
£Ø1£©ĒóÖ¤£ŗ![]() £»
£»
£Ø2£©Čē¹ū![]() £¬ĒóÖ¤£ŗ
£¬ĒóÖ¤£ŗ![]() .
.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗ”÷AOBŗĶ”÷COD¾łĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬”ĻAOB£½”ĻCOD£½90”ć£®Į¬½ÓAD£¬BC£¬µćHĪŖBCÖŠµć£¬Į¬½ÓOH£®

£Ø1£©ČēĶ¼1ĖłŹ¾£¬ČōAB£½8£¬CD£½2£¬ĒóOHµÄ³¤£»
£Ø2£©½«”÷CODČʵćOŠż×ŖŅ»¶ØµÄ½Ē¶Čµ½Ķ¼2ĖłŹ¾Ī»ÖĆŹ±£¬Ļ߶ĪOHÓėADÓŠŌõŃłµÄŹżĮæŗĶĪ»ÖĆ¹ŲĻµ£¬²¢Ö¤Ć÷ÄćµÄ½įĀŪ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŌDĪŖ¶„µćµÄÅ×ĪļĻßy=©x2+bx+c½»xÖįÓŚA”¢BĮ½µć£¬½»yÖįÓŚµćC£¬Ö±ĻßBCµÄ±ķ“ļŹ½ĪŖy=©x+3£®
£Ø1£©ĒóÅ×ĪļĻߵıķ“ļŹ½£»
£Ø2£©ŌŚÖ±ĻßBCÉĻÓŠŅ»µćP£¬Ź¹PO+PAµÄÖµ×īŠ”£¬ĒóµćPµÄ×ų±ź£»
£Ø3£©ŌŚxÖįÉĻŹĒ·ń“ęŌŚŅ»µćQ£¬Ź¹µĆŅŌA”¢C”¢QĪŖ¶„µćµÄČż½ĒŠĪÓė”÷BCDĻąĖĘ£æČō“ęŌŚ£¬ĒėĒó³öµćQµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
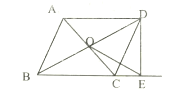
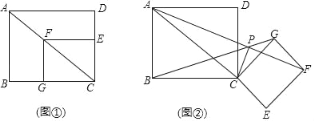
”¾ĢāÄæ”æČēĶ¼¢Ł£¬ĖıߊĪABCDÓėĖıߊĪCEFG¶¼ŹĒ¾ŲŠĪ£¬µćE£¬G·Ö±šŌŚ±ßCD£¬CBÉĻ£¬µćFŌŚACÉĻ£¬AB£½3£¬BC£½4
£Ø1£©Ēó![]() µÄÖµ£»
掙术
£Ø2£©°Ń¾ŲŠĪCEFGČʵćCĖ³Ź±ÕėŠż×Ŗµ½Ķ¼¢ŚµÄĪ»ÖĆ£¬PĪŖAF£¬BGµÄ½»µć£¬Į¬½ÓCP
£Ø¢ń£©Ēó![]() µÄÖµ£»
掙术
£Ø¢ņ£©ÅŠ¶ĻCPÓėAFµÄĪ»ÖĆ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com