
【题目】(定义)配方法是指将一个式子或一个式子的某一部分通过恒等变形化为完全平方式或几个完全平
方式的和,这种方法称之为配方法,例如:可将多项式![]() 通过横档变形化为
通过横档变形化为![]() 的形式,这个变形过程中应用了配方法.
的形式,这个变形过程中应用了配方法.
(1)(理解)对于多项式![]() ,当x=____________时,它的最小值为______________.
,当x=____________时,它的最小值为______________.
(2)(应用)若![]() ,求
,求![]() 的值.
的值.
(3)(拓展)![]() 是
是![]() 的三边,且有
的三边,且有![]() .
.
①若c为整数,求c的值.
②直接写出这个三角形的周长.
【答案】(1)2;1;(2)![]() ;(3)①4或5或6;②当三边分别为2,5,4时,周长为11,当三边分别为2,5,5时,周长为12,当三边分别为2,5,6时,周长为13
;(3)①4或5或6;②当三边分别为2,5,4时,周长为11,当三边分别为2,5,5时,周长为12,当三边分别为2,5,6时,周长为13
【解析】
(1)【理解】根据配方法可以说明x24x+5的最小值为1;
(2)【应用】将原式拆分,组成两个完全平方式,再根据非负数的性质即可求出a、b的值,代入ab计算即可;
(3)【拓展】①利用配方法和三角形的三边关系求得c的值;②个根据c值写出这个三角形的周长.
(1)【理解】x24x+5=x24x+22+1=(x2)2+1,
所以当x=2时,x24x+5的最小值是1.
故答案是:2;1;
(2)【应用】∵![]() ,
,
∴a2+2ab+b2+b2+4b+4=0,
∴![]() ,
,
∴a+b=0,b+2=0,
解得a=2,b=2.
∴ba=(2)2=4;
(3)【拓展】①∵a2+b2=4a+10b29,
∴a2+b24a10b+29=0,
∴a24a+4+b210b+25=0,
∴(a2)2+(b5)2=0,
∴a2=0,b5=0,
解得a=2,b=5,
∴3<c<7,
∵c为整数,
∴c的值为4,5,6;
②当三边分别为2,5,4时,周长为11;
当三边分别为2,5,5时,周长为12;
当三边分别为2,5,6时,周长为13.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】给出下列4个命题:①两边及其中一边上的中线对应相等的两个三角形全等;②两边及其中一边上的高对应相等的两个三角形全等;③两边及一角对应相等的两个三角形全等;④有两角及其中一角的角平分线对应相等的两个三角形全等.其中正确的的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接“国家卫生城市”复检,某市环卫局准备购买![]() 、
、![]() 两种型号的垃圾箱,通过市场调研得知:购买3个
两种型号的垃圾箱,通过市场调研得知:购买3个![]() 型垃圾箱和2个
型垃圾箱和2个![]() 型垃圾箱共需540元;购买2个
型垃圾箱共需540元;购买2个![]() 型垃圾箱比购买3个
型垃圾箱比购买3个![]() 型垃圾箱少用160元.
型垃圾箱少用160元.
(1)每个![]() 型垃圾箱和
型垃圾箱和![]() 型垃圾箱各多少元?
型垃圾箱各多少元?
(2)现需要购买![]() ,
,![]() 两种型号的垃圾箱共300个,设购买
两种型号的垃圾箱共300个,设购买![]() 型垃圾箱
型垃圾箱![]() 个,购买
个,购买![]() 型垃圾箱和
型垃圾箱和![]() 型垃圾箱的总费用为
型垃圾箱的总费用为![]() 元,求
元,求![]() 与
与![]() 的函数表达式.如果购买
的函数表达式.如果购买![]() 型垃圾箱是
型垃圾箱是![]() 型垃圾箱的2倍,求购买
型垃圾箱的2倍,求购买![]() 型垃圾箱和
型垃圾箱和![]() 型垃圾箱的总费用.
型垃圾箱的总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
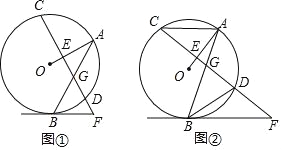
【题目】在⊙O中,弦AB与弦CD相交于点G,OA⊥CD于点E,过点B作⊙O的切线BF交CD的延长线于点F.
(I)如图①,若∠F=50°,求∠BGF的大小;
(II)如图②,连接BD,AC,若∠F=36°,AC∥BF,求∠BDG的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
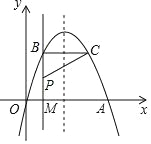
【题目】如图,经过原点的抛物线y=﹣x2+2mx(m>0)与x轴的另一个交点为A,过点P(1,m)作直线PA⊥x轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(点B、C不重合),连接CB、CP.
(I)当m=3时,求点A的坐标及BC的长;
(II)当m>1时,连接CA,若CA⊥CP,求m的值;
(III)过点P作PE⊥PC,且PE=PC,当点E落在坐标轴上时,求m的值,并确定相对应的点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
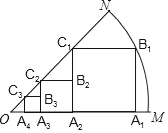
【题目】如图所示,扇形OMN的圆心角为45°,正方形A1B1C1A2的边长为2,顶点A1,A2在线段OM上,顶点B1在弧MN上,顶点C1在线段ON上,在边A2C1上取点B2,以A2B2为边长继续作正方形A2B2C2A3,使得点C2在线段ON上,点A3在线段OM上,……,依次规律,继续作正方形,则A2018M=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
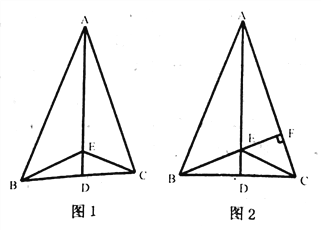
【题目】如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上,连接BE、CE.
(1)求证:BE=CE
(2)如图2,若BE的延长线交AC于点F,且BF ⊥AC,垂足为F,原题设其它条件不变.求证:∠CAD=∠CBF
(3)在(2)的条件下,若∠BAC=45![]() ,判断△CFE的形状,并说明理由.
,判断△CFE的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com