
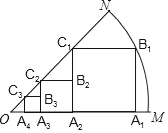
【题目】如图所示,扇形OMN的圆心角为45°,正方形A1B1C1A2的边长为2,顶点A1,A2在线段OM上,顶点B1在弧MN上,顶点C1在线段ON上,在边A2C1上取点B2,以A2B2为边长继续作正方形A2B2C2A3,使得点C2在线段ON上,点A3在线段OM上,……,依次规律,继续作正方形,则A2018M=__________.
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,BC交直径AD于点E,过点C作AD的垂线交AB的延长线于点G,垂足为F.连接OC.
(1)若∠G=48°,求∠ACB的度数;
(2)若AB=AE,求证:∠BAD=∠COF;
(3)在(2)的条件下,连接OB,设△AOB的面积为S1,△ACF的面积为S2.若tan∠CAF=![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(定义)配方法是指将一个式子或一个式子的某一部分通过恒等变形化为完全平方式或几个完全平
方式的和,这种方法称之为配方法,例如:可将多项式![]() 通过横档变形化为
通过横档变形化为![]() 的形式,这个变形过程中应用了配方法.
的形式,这个变形过程中应用了配方法.
(1)(理解)对于多项式![]() ,当x=____________时,它的最小值为______________.
,当x=____________时,它的最小值为______________.
(2)(应用)若![]() ,求
,求![]() 的值.
的值.
(3)(拓展)![]() 是
是![]() 的三边,且有
的三边,且有![]() .
.
①若c为整数,求c的值.
②直接写出这个三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
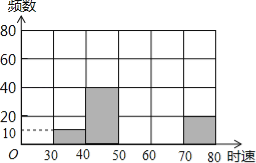
【题目】将某雷达测速区监测到的一组汽车的时速数据整理,得到其频数分布表(未完成):
数据段 | 30~40 | 40~50 | 50~60 | 60~70 | 70~80 | 总计 |
频 数 | 10 | 40 | | | 20 | |
百分比 | 5% | | 40% | | 10% | |
注:30~40为时速大于等于30千米而小于40千米,其他类同.
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果此路段汽车时速超过60千米即为违章,则违章车辆共有多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距80km,一辆汽车上午9:00从甲地出发驶往乙地,匀速行驶了一半的路程后将速度提高了20km/h,并继续匀速行驶至乙地,汽车行驶的路程y(km)与时间x(h)之间的函数关系如图所示,该车到达乙地的时间是当天上午( )
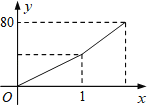
A. 10:35 B. 10:40 C. 10:45 D. 10:50
查看答案和解析>>
科目:初中数学 来源: 题型:
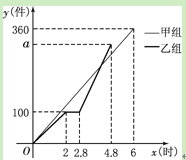
【题目】甲、乙两组工人同时加工某种零件,乙组工作中有一次停产更换设备,更换设备
后,乙组的工作效率是原来的2倍.两组各自加工零件的数量![]() (件)与时间
(件)与时间![]() (时)的函数图
(时)的函数图
象如图所示.
(1)求甲组加工零件的数量y与时间![]() 之间的函数关系式.(2分)
之间的函数关系式.(2分)
(2)求乙组加工零件总量![]() 的值.(3分)
的值.(3分)
(3)甲、乙两组加工出的零件合在一起装箱,每够300件装一箱,零件装箱的时间忽略不计,求经过多长时间恰好装满第1箱?再经过多长时间恰好装满第2箱?(5分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个被平均分成![]() 等份的转盘,每一个扇形中都标有相应的数字,甲乙两人分别转动转盘,设甲转动转盘后指针所指区域内的数字为
等份的转盘,每一个扇形中都标有相应的数字,甲乙两人分别转动转盘,设甲转动转盘后指针所指区域内的数字为![]() ,乙转动转盘后指针所指区域内的数字为
,乙转动转盘后指针所指区域内的数字为![]() (当指针在边界上时,重转一次,直到指向一个区域为止).
(当指针在边界上时,重转一次,直到指向一个区域为止).
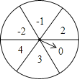
![]() 直接写出甲转动转盘后所指区域内的数字为负数的概率;
直接写出甲转动转盘后所指区域内的数字为负数的概率;
![]() 用树状图或列表法,求出点
用树状图或列表法,求出点![]() 落在第二象限内的概率.
落在第二象限内的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
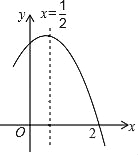
【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=![]() ,且经过点(2,0),下列说法:①abc<0;②﹣2b+c=0;③4a+2b+c<0;④若(
,且经过点(2,0),下列说法:①abc<0;②﹣2b+c=0;③4a+2b+c<0;④若(![]() ,y1)、(
,y1)、(![]() ,y2)是抛物线上的两点,则y1<y2;⑤
,y2)是抛物线上的两点,则y1<y2;⑤![]() >m(am+b)(其中m≠
>m(am+b)(其中m≠![]() ).其中说法正确的是_____
).其中说法正确的是_____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com