练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在中，，点是的中点.在和上.分别有一动点，在移动过程中保持.

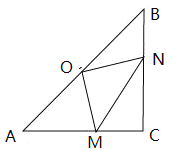
    （1）判断的形状，并说明理出.

    （2）当时，求四边形的面积.

    【答案】（1）等腰直角三角形，见解析；（2）

    【解析】

    连接OC.先证得△OAM≌△CNO，然后根据全等三角形的对应边相等推知OM=ON；然后由等腰直角三角形ABC的性质、等腰三角形OMN的性质推知∠NOM=90°，即△OMN是等腰直角三角形；

    （2）由（1）得△OAM≌△CNO，所以四边形的面积等于△OAC的面积，根据题意可得OC=OA =AB=5，从而求解.

    解: (1)是等腰直角三角形.理由如下:

    连接.

    ，点是的中点，

    (三线合一)

    .

    .

    .

    ，

    .

    .

    .

    是等腰直角三角形.

    (2)∵AB=10,∴OC=AB=5=OA,

    由(1)，，OC⊥AAB，

    .

    .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为迎接“国家卫生城市”复检，某市环卫局准备购买、两种型号的垃圾箱，通过市场调研得知：购买3个型垃圾箱和2个型垃圾箱共需540元；购买2个型垃圾箱比购买3个型垃圾箱少用160元．

    (1)每个型垃圾箱和型垃圾箱各多少元？

    (2)现需要购买，两种型号的垃圾箱共300个，设购买型垃圾箱个，购买型垃圾箱和型垃圾箱的总费用为元，求与的函数表达式．如果购买型垃圾箱是型垃圾箱的2倍，求购买型垃圾箱和型垃圾箱的总费用．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，扇形OMN的圆心角为45°，正方形A1B1C1A2的边长为2，顶点A1，A2在线段OM上，顶点B1在弧MN上，顶点C1在线段ON上，在边A2C1上取点B2，以A2B2为边长继续作正方形A2B2C2A3，使得点C2在线段ON上，点A3在线段OM上，……，依次规律，继续作正方形，则A2018M=__________．

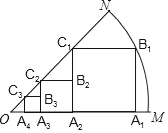
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个不透明袋子中有1个红球和n个白球，这些球除颜色外无其他差别．

    （1）当n=l时，从袋中随机摸出1个球，摸到红球与摸到白球的可能性是否相同？ （填“相同”或“不相同”）

    （2）从袋中随机摸出1个球，记录其颜色，然后放回，大量重复该实验，发现摸到红球的频率稳定于0.25，则n的值是 ；

    （3）当n=2时，请用列表或画树状图的方法求两次摸出的球颜色不同的概率（摸出一个球，不放回，然后再摸一个球）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中，点E到AD，AB，BC三边的距离都相等，则∠AEB（　　）

    A.是锐角B.是直角C.是钝角D.度数不确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AC与BD相交于点O，∠D=∠C，添加下列哪个条件后，仍不能使△ADO≌△BCO的是（　　）

    A. AD=BC B. AC=BD C. OD=OC D. ∠ABD=∠BAC

    查看答案和解析>>

    科目：初中数学 来源： 题型：

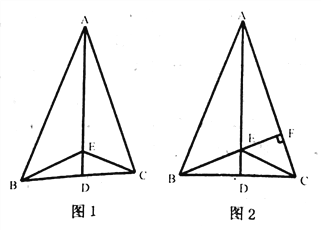
    【题目】如图1，在△ABC中，AB=AC，点D是BC的中点，点E在AD上，连接BE、CE.

    (1)求证：BE=CE

    (2)如图2，若BE的延长线交AC于点F，且BF ⊥AC，垂足为F，原题设其它条件不变．求证：∠CAD=∠CBF

    (3)在(2)的条件下，若∠BAC=45，判断△CFE的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2019年4月，第二届“一带一路”国际合作高峰论坛在北京举行，共签署了总额640多亿美元的项目合作协议。某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区，已知2件甲种商品与3件乙商品的销售收入相同，3件甲种商品比2件乙种商品的销售收入多1500元.

    （1）甲种商品与乙种商品的销售单价各是多少元？（列二元一次方程组解应用题）

    （2）设甲、乙两种商品的销售总收入为万元，销售甲种商品万件，

    ①写出与之间的函数关系式；

    ②若甲、乙两种商品的销售收入为5400万元，则销售甲种商品多少万件？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，Rt△OAB的直角顶点A在x轴的正半轴上，若顶点B的纵坐标为2，∠B＝60°，OC＝AC．

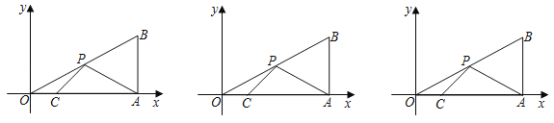
    （1）请写出A、B、C三点的坐标；

    （2）点P是斜边OB上的一个动点，则△PAC的周长的最小值为多少？

    （3）若点P是OB的中点，点E在AO边上，将△OPE沿PE翻折，使得点O落在O'处，当O'E⊥AC时，在坐标平面内是否存在一点Q，使得△BAQ≌△O′PE，若存在，请直接写出Q点坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案