
【题目】如图1,在△ABC中,AB=AC=20,tanB=![]() ,点D为BC边上的动点(D不与点B,C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F,连接CF.
,点D为BC边上的动点(D不与点B,C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F,连接CF.
(1)求证:△ABD∽△DCE;
(2)当DE∥AB时(如图2),求AE的长;
(3)点D在BC边上运动的过程中,是否存在某个位置,使得DF=CF?若存在,求出此时BD的长;若不存在,请说明理由.
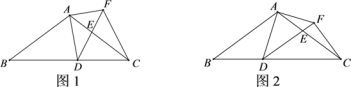
【答案】(1)详见解析;(2)![]() ;(3)点D在BC边上运动 的过程中,存在某个位置,使得DF=CF,此时BD=18.
;(3)点D在BC边上运动 的过程中,存在某个位置,使得DF=CF,此时BD=18.
【解析】
(1)根据两角对应相等的两个三角形相似证明即可;
(2)解直角三角形求出BC,由△ABD∽△DCE,推出![]() =
=![]() ,可得DB=
,可得DB=![]() =
=![]() =
=![]() ,由DE∥AB,推出
,由DE∥AB,推出![]() =
=![]() ,求出AE即可;
,求出AE即可;
(3)点D在BC边上运动的过程中,存在某个位置,使得DF=CF.过点F作FH⊥BC于点H,过点A作AM⊥BC于点M,AN⊥FH于点N,则∠NHA=∠AMH=∠ANH=90°,由△AFN∽△ADM,可得![]() =
=![]() =tan∠ADF=tanB=
=tan∠ADF=tanB=![]() ,推出CH=CM-MH=CM-AN=16-9=7,再利用等腰三角形的性质,求出CD即可解决问题.
,推出CH=CM-MH=CM-AN=16-9=7,再利用等腰三角形的性质,求出CD即可解决问题.
解:(1)∵AB=AC,
∴∠B=∠ACB.
∵∠ADE+∠CDE=∠B+∠BAD,∠ADE=∠B,
∴∠BAD=∠CDE.
∴△ABD∽△DCE.
(2)过点A作AM⊥BC于点M.
在Rt△ABM中,设BM=4k,则AM=BM·tanB=4k·![]() =3k.
=3k.
由勾股定理,得:AB2=AM2+BM2,得:
202=(3k)2+(4k)2,解得:k=4.
∵AB=AC,AM⊥BC,
∴BC=2BM=8k=32.
∵DE∥AB,
∴∠BAD=∠ADE.
又∵∠ADE=∠B,∠B=∠ACB,
∴∠BAD=∠ACB.
∵∠ABD=∠CBA,
∴△ABD∽△CBA,
∴![]() =
=![]() ,则DB=
,则DB=![]() =
=![]() =
=![]() .
.
∵DE∥AB,
∴![]() =
=![]() ,
,
∴AE=![]() =
=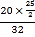 =
=![]() .
.
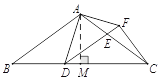
(3)点D在BC边上运动的过程中,存在某个位置,使得DF=CF.
过点F作FH⊥BC于点H,过点A作AM⊥BC于点M,AN⊥FH于点N,则∠NHA=∠AMH=∠ANH=90°.
∴四边形AMHN为矩形.
∴∠MAN=90°,MH=AN.
∵AB=AC,AM⊥BC,
∴BM=CM=![]() BC=
BC=![]() ×32=16.
×32=16.
在Rt△ABM中,由勾股定理,得:AM=![]() =
=![]() =12.
=12.
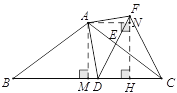
∵AN⊥FH,AM⊥BC,
∴∠ANF=90°=∠AMD.
∵∠DAF=90°=∠MAN,
∴∠NAF=∠MAD,
∴△AFN∽△ADM.
∴![]() =
=![]() =tan∠ADF=tanB=
=tan∠ADF=tanB=![]() .
.
∴AN=![]() AM=
AM=![]() ×12=9.
×12=9.
∴CH=CM-MH=CM-AN=16-9=7.
当DF=CF时,由点D不与点C重合时,可知△DFC为等腰三角形.
又∵FH⊥DC,
∴CD=2CH=14.
∴BD=BC-CD=32-14=span>18.
∴点D在BC边上运动 的过程中,存在某个位置,使得DF=CF,此时BD=18.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
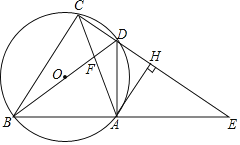
【题目】如图,四边形ABCD的顶点在⊙O上,BD是⊙O的直径,延长CD、BA交于点E,连接AC、BD交于点F,作AH⊥CE,垂足为点H,已知∠ADE=∠ACB.
(1)求证:AH是⊙O的切线;
(2)若OB=4,AC=6,求sin∠ACB的值;
(3)若![]() ,求证:CD=DH.
,求证:CD=DH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )

A. ∠BCA=∠F; B. ∠B=∠E; C. BC∥EF ; D. ∠A=∠EDF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC 的顶点分别为 A(-2,2)、B(-4,5)、C(-5,1)和直线 m (直线 m 上各点的横坐标都为 1).
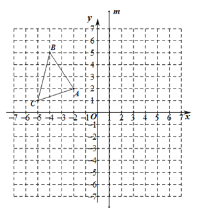
(1)作出△ABC 关于 ![]() 轴对称的图形△A1B1C1,并写出点 A1 的坐标;
轴对称的图形△A1B1C1,并写出点 A1 的坐标;
(2)作出点 C关于直线 m 对称的点C2 , 并写出点C2 的坐标;
(3)在![]() 轴上找一点P,使 PA+PC的值最小,请直接写出点P的坐标.
轴上找一点P,使 PA+PC的值最小,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=|a|x2+bx+c的图象经过A(m,n)、B(0,y1)、C(3-m,n)、D(![]() , y2)、E(2,y3),则y1、y2、y3的大小关系是( ).
, y2)、E(2,y3),则y1、y2、y3的大小关系是( ).
A. y1< y2< y3B. y1 < y3< y2C. y3< y2< y1D. y2< y3< y1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】月饼是中华民族的传统美食,在中秋节期间,小邱家买了三种不同馅的月饼,分别是:肉松月饼(记为![]() ),豆沙月饼(记为
),豆沙月饼(记为![]() ),莲蓉月饼(记为
),莲蓉月饼(记为![]() ).这些月饼除了馅不同,其余均相同.小邱的妈妈在一个盘子中放入了一个肉松月饼,一个豆沙月饼和两个莲蓉月饼.根据以上情况,请你回答下列问题
).这些月饼除了馅不同,其余均相同.小邱的妈妈在一个盘子中放入了一个肉松月饼,一个豆沙月饼和两个莲蓉月饼.根据以上情况,请你回答下列问题
(1)假设小邱从盘子中随机取一个月饼恰好取到肉松月饼概率是多少?
(2)若小邱先从盘子中随机取一个月饼,吃完后再随机取一个,请用列表法或画树状图法求小邱取到的两个月饼中至少有一个是莲蓉月饼的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业1~5月份利润的变化情况图所示,以下说法与图中反映的信息相符的是( )
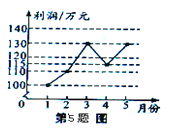
A. 1~2月份利润的增长快于2~3月份分利润的增长
B. 1~4月份利润的极差与1~5月份利润的极差不同
C. 1~5月份利润的的众数是130万元
D. 1~5月份利润的中位数为120万元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),矩形![]() 的一边
的一边![]() 在直角坐标系中
在直角坐标系中![]() 轴上,折叠边
轴上,折叠边![]() ,使点
,使点![]() 落在
落在![]() 轴上点
轴上点![]() 处,折痕为
处,折痕为![]() ,已知
,已知![]() ,
,![]() ,并设点
,并设点![]() 坐标为
坐标为![]() ,其中
,其中![]() .
.
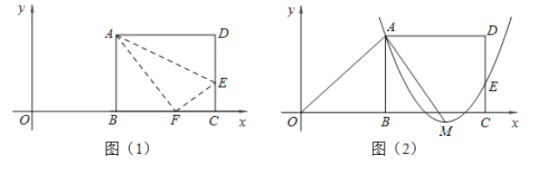
(1)求点![]() 、
、![]() 的坐标(用含
的坐标(用含![]() 的式子表示);
的式子表示);
(2)连接![]() ,若
,若![]() 是等腰三角形,求
是等腰三角形,求![]() 的值;
的值;
(3)如图(2),设抛物线![]() 经过A、E两点,其顶点为
经过A、E两点,其顶点为![]() ,连接AM,若
,连接AM,若![]() ,求
,求![]() 、
、![]() 、
、![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华和小丽设计了A、B两种游戏:游戏A的规则是:用3张数字分别是2、3、4的扑克牌,将牌洗匀后背面朝上放置在桌面上,第一次随机抽出一张牌记下数字后再原样放回,洗匀后再第二次随机抽出一张牌记下数字,若抽出的两张牌上的数字之和为偶数,则小华获胜;若两数字之和为奇数,则小丽获胜.游戏B的规则是:用4张数字分别是5、6、8、8的扑克牌,将牌洗匀后背面朝上放置在桌面上,小华先随机抽出一张牌,抽出的牌不放回,小丽从剩下的牌中再随机抽出一张牌,若小华抽出的牌面上的数字比小丽抽出的牌面上的数字大,则小华获胜,否则小丽获胜.请你帮小丽选择其中一种游戏,使她获胜的可能性较大,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com