
【题目】如图(1),矩形![]() 的一边
的一边![]() 在直角坐标系中
在直角坐标系中![]() 轴上,折叠边
轴上,折叠边![]() ,使点
,使点![]() 落在
落在![]() 轴上点
轴上点![]() 处,折痕为
处,折痕为![]() ,已知
,已知![]() ,
,![]() ,并设点
,并设点![]() 坐标为
坐标为![]() ,其中
,其中![]() .
.
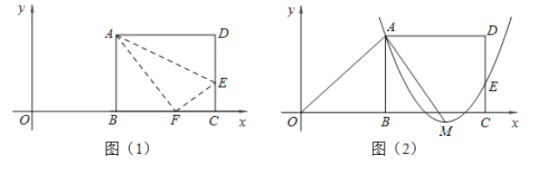
(1)求点![]() 、
、![]() 的坐标(用含
的坐标(用含![]() 的式子表示);
的式子表示);
(2)连接![]() ,若
,若![]() 是等腰三角形,求
是等腰三角形,求![]() 的值;
的值;
(3)如图(2),设抛物线![]() 经过A、E两点,其顶点为
经过A、E两点,其顶点为![]() ,连接AM,若
,连接AM,若![]() ,求
,求![]() 、
、![]() 、
、![]() 的值.
的值.
【答案】(1)点![]() 、
、![]() 的坐标是
的坐标是![]() ;(2)m的值是6,4,
;(2)m的值是6,4,![]() ;(3)a、h、m的值是
;(3)a、h、m的值是![]() ,-1,12.
,-1,12.
【解析】
(1)根据四边形ABCD是矩形以及由折叠对称性得出AF=AD=10,EF=DE,进而求出BF的长,即可得出E,F点的坐标;
(2)分三种情况讨论:若AO=AF,OF=FA,AO=OF,利用勾股定理求出即可;
(3)由E(m+10,3),A(m,8),代入二次函数解析式得出M点的坐标,再利用△AOB∽△AMG,求出m的值即可.
解:(1)∵四边形ABCD是矩形,
∴AD=CB=10,AB=DC=8,∠D=∠DCB=∠ABC=90°,
由折叠对称性:AF=AD=10,EF=DE,
在Rt△ABF中,BF=![]() =6,
=6,
∴CF=4,
设EF=x,则EC=8-x,
在Rt△ECF中,42+(8-x)2=x2,
解得:x=5,
∴CE=3,
∵B(m,0),
∴E(m+10,3),F(m+6,0);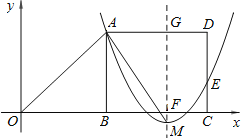
(2)分三种情况讨论:
若AO=AF,
∵AB⊥OF,
∴BO=BF=6,
∴m=6,
若OF=FA,则m+6=10,
解得:m=4,
若AO=OF,在Rt△AOB中,AO2=OB2+AB2=m2+64,
∴(m+6)2=m2+64,
解得:m=![]() ,
,
∴m=6或4或![]() ;
;
(3)由(1)知:E(m+10,3),A(m,8).
∴![]() ,
,
得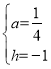 ,
,
∴M(m+6,-1),
设对称轴交AD于G,
∴G(m+6,8),
∴AG=6,GM=8-(-1)=9,
∵∠OAB+∠BAM=90°,∠BAM+∠MAG=90°,
∴∠OAB=∠MAG,
∵∠ABO=∠MGA=90°,
∴△AOB∽△AMG,
∴![]() ,
,
即:![]() ,
,
∴m=12.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
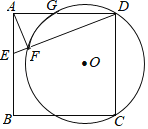
【题目】如图,正方形ABCD中,E为AB上一点,AF⊥DE于点F,已知DF=5EF=5,过C、D、F的⊙O与边AD交于点G,则DG=( )
A.2![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC=20,tanB=![]() ,点D为BC边上的动点(D不与点B,C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F,连接CF.
,点D为BC边上的动点(D不与点B,C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F,连接CF.
(1)求证:△ABD∽△DCE;
(2)当DE∥AB时(如图2),求AE的长;
(3)点D在BC边上运动的过程中,是否存在某个位置,使得DF=CF?若存在,求出此时BD的长;若不存在,请说明理由.
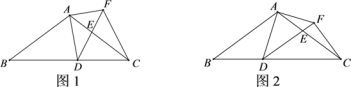
查看答案和解析>>
科目:初中数学 来源: 题型:
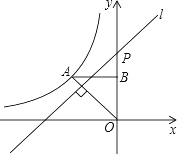
【题目】如图,反比例函数y=![]() (x<0)的图象经过点A(﹣2,2),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是________.
(x<0)的图象经过点A(﹣2,2),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,坐标原点O是菱形ABOC的一个顶点,边OB落在x轴的负半轴上,且cos∠BOC=![]() ,顶点C的坐标为(a,4),反比例函数
,顶点C的坐标为(a,4),反比例函数![]() 的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为拓宽学生视野,引导学生主动适应社会,促进书本知识和生活经验的深度融合,我市某中学决定组织部分班级去赤壁开展研学旅行活动,在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生.现有甲、乙两种大客车,它们的载客量和租金如表所示.
甲种客车 | 乙种客车 | |
载客量/(人/辆) | 30 | 42 |
租金/(元/辆) | 300 | 400 |
学校计划此次研学旅行活动的租车总费用不超过3100元,为了安全,每辆客车上至少要有2名老师.
(1)参加此次研学旅行活动的老师和学生各有多少人?
(2)既要保证所有师生都有车坐,又要保证每辆客车上至少要有2名老师,可知租用客车总数为 辆;
(3)你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 分别是边
分别是边![]() 的中点,连接
的中点,连接![]() .将
.将![]() 绕点
绕点![]() 顺时针方向旋转,记旋转角为
顺时针方向旋转,记旋转角为![]() .
.
①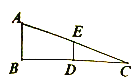 ②
②
③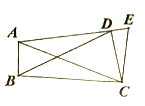 ④
④
(1)问题发现:当![]() 时,
时,![]() .
.
(2)拓展探究:试判断:当![]() 时,
时,![]() 的大小有无变化?请仅就图②的情况给出证明.
的大小有无变化?请仅就图②的情况给出证明.
(3)问题解决:当![]() 旋转至
旋转至![]() 三点共线时,如图③,图④,直接写出线段
三点共线时,如图③,图④,直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() 为二次函数图象上任一点.
为二次函数图象上任一点.
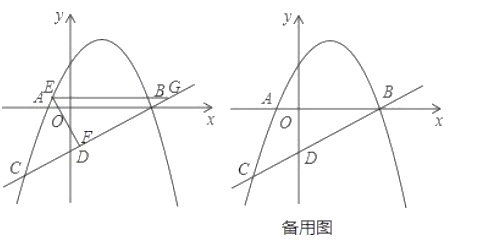
![]() 求这个二次函数的解析式;
求这个二次函数的解析式;
![]() 若点
若点![]() 是直线
是直线![]() 上方抛物线上一点,过
上方抛物线上一点,过![]() 分别作
分别作![]() 和
和![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于不同的两点
于不同的两点![]() 在
在![]() 的左侧),求
的左侧),求![]() 周长的最大值;
周长的最大值;
![]() 是否存在点
是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为直角边的直角三角形?如果存在,求点
为直角边的直角三角形?如果存在,求点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com