
【题目】如图,半径为2的⊙O分别与x轴,y轴交于A,D两点,⊙O上两个动点B,C,使∠BAC=60°恒成立,设△ABC的重心为G,则DG的最小值是_______.

【答案】![]() ﹣
﹣![]()
【解析】
连接AG并延长,交BC于点F,由△ABC的重心为G,可知F为BC的中点,再由垂径定理可知OF⊥BC,从而可求得OF的长;在AO上取点E,使AE=![]() AO,连接GE,可判定△AGE∽△AFO,由相似三角形的性质列出比例式,求得GE的长,进而可得点E的坐标,利用勾股定理求出DE的长,根据G在以E为圆心,
AO,连接GE,可判定△AGE∽△AFO,由相似三角形的性质列出比例式,求得GE的长,进而可得点E的坐标,利用勾股定理求出DE的长,根据G在以E为圆心,![]() 为半径的圆上运动,可知DG的最小值为DE的长减去
为半径的圆上运动,可知DG的最小值为DE的长减去![]() ,计算即可.
,计算即可.
解:连接AG并延长,交BC于点F,
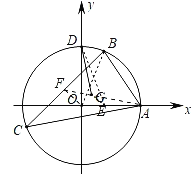
∵△ABC的重心为G,
∴F为BC的中点,
∴OF⊥BC,
∵∠BAC=60°,
∴∠BOF=60°,
∴∠OBF=30°,
∴OF=![]() OB=1,
OB=1,
∵△ABC的重心为G,
∴AG=![]() AF,
AF,
在AO上取点E,使AE=![]() AO,连接GE,
AO,连接GE,
∵![]() =
=![]() =
=![]() ,∠FAO=∠GAE,
,∠FAO=∠GAE,
∴△AGE∽△AFO,
∴![]() =
=![]() ,
,
∴GE=![]() .
.
∴G在以E为圆心,![]() 为半径的圆上运动,
为半径的圆上运动,
∴E(![]() ,0),
,0),
∴DE=![]() =
=![]() ,
,
∴DG的最小值是![]() ﹣
﹣![]() ,
,
故答案为:![]() ﹣
﹣![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在下列![]() 网格中,横、纵坐标均是整数的点叫格点,例如
网格中,横、纵坐标均是整数的点叫格点,例如![]() 都是格点.
都是格点.
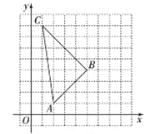
(1)直接写出![]() 的面积;
的面积;
(2)仅用无刻度的直尺在图中画出一条线段![]() ,使它满足以下条件:①
,使它满足以下条件:①![]() 点在
点在![]() 内;②点
内;②点![]() 都是格点;③
都是格点;③![]() 三等分
三等分![]() ;④
;④![]() ,请写出点
,请写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
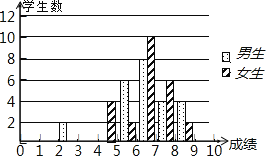
【题目】为了迎接体育中考,初三7班的体育老师对全班48名学生进行了一次体能模拟测试,得分均为整数,满分10分,成绩达到6分以上(包括6分)为合格,成绩达到9分以上(包括9分)为优秀,这次模拟测试中男、女生全部成绩分布的条形统计图如下
(1)请补充完成下面的成绩统计分析表:
平均分 | 方差 | 中位数 | 合格率 | 优秀率 | |
男生 | 6.9 | 2.4 | ______ | 91.7% | 16.7% |
女生 | ______ | 1.3 | ______ | 83.3% | 8.3% |
(2)男生说他们的合格率、优秀率均高于女生,所以他们的成绩好于女生,但女生不同意男生的说法,认为女生的成绩要好于男生,请给出两条支持女生观点的理由;
(3)体育老师说,咱班的合格率基本达标,但优秀率太低,我们必须加强体育锻炼,两周后的目标是:全班优秀率达到50%.如果女生新增优秀人数恰好是男生新增优秀人数的两倍,那么男、女生分别新增多少优秀人数才能达到老师的目标?
查看答案和解析>>
科目:初中数学 来源: 题型:
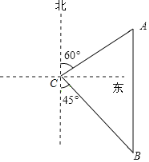
【题目】如图,一艘轮船从位于灯塔![]() 的北偏东60°方向,距离灯塔60海里的小岛
的北偏东60°方向,距离灯塔60海里的小岛![]() 出发,沿正南方向航行一段时间后,到达位于灯塔
出发,沿正南方向航行一段时间后,到达位于灯塔![]() 的南偏东45°方向上的
的南偏东45°方向上的![]() 处,这时轮船
处,这时轮船![]() 与小岛
与小岛![]() 的距离是__________海里.
的距离是__________海里.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,O是△ABC所在平面上的动点,连接OB,OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.

(1)如图,当点O在△ABC的内部时,求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,点O所在位置应满足什么条件?(直接写出答案不需要说明理由.)
(3)在图2中作出点O,使得四边形DGFE是正方形(保留作图痕迹,不写作法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“前线医护人员”和全国人民的共同努力下,疫情得到了有效控制,宁波各大企业复工复产有序进行.为了实现员工“一站式”返岗,宁波某企业打算租赁5辆客车前往宁波东站接员工返岗.已知现有A、B两种客车,A型客车的载客量为45人/辆,每辆租金为400元;B型客车的载客量为30人/辆,每辆租金为280元.设租用A型客车为x辆,所需费用为y元.
(1)求y关于x的函数解析式;
(2)若该企业需要接的员工有205人,请求出租车费用最小值,并写出对应的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的顶点A,B在x轴的负半轴上,反比例函数y=![]() (k1≠0)在第二象限内的图象经过正方形ABCD的顶点D(m,2)和BC边上的点G(n,
(k1≠0)在第二象限内的图象经过正方形ABCD的顶点D(m,2)和BC边上的点G(n,![]() ),直线y=k2x+b(k2≠0)经过点D,点G,则不等式
),直线y=k2x+b(k2≠0)经过点D,点G,则不等式![]() ≤k2x+b的解集为__________.
≤k2x+b的解集为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
如图1,![]() 和
和![]() 均为等边三角形,点
均为等边三角形,点![]() ,
,![]() ,
,![]() 在同一条直线上,连接
在同一条直线上,连接![]() ;
;
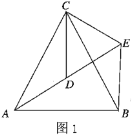
探究发现
(1)善思组发现:![]() ,请你帮他们写出推理过程;
,请你帮他们写出推理过程;
(2)钻研组受善思组的启发,求出了![]() 度数,请直接写出
度数,请直接写出![]() 等于______度;
等于______度;
(3)奋进组在前面两组的基础上又探索出了![]() 与
与![]() 的位置关系为______(请直接写出结果);
的位置关系为______(请直接写出结果);
拓展探究
(4)如图2,![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,点
,点![]() ,
,![]() ,
,![]() 在同一条直线上,
在同一条直线上,![]() 为
为![]() 中
中![]() 边上的高,连接
边上的高,连接![]() ,试探究
,试探究![]() ,
,![]() ,
,![]() 之间有怎样的数量关系.
之间有怎样的数量关系.
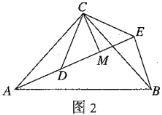
创新组类比善思组的发现,很快证出![]() ,进而得出
,进而得出![]() .请你写出
.请你写出![]() ,
,![]() ,
,![]() 之间的数量关系并帮创新组完成后续的证明过程.
之间的数量关系并帮创新组完成后续的证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示, 在平面直角坐标系中, 边长为![]() 的正方形
的正方形![]() 的边
的边![]() 在
在![]() 轴上,
轴上, ![]() 交
交![]() 轴于点
轴于点![]() ,一次函数
,一次函数![]() 的图像经过点
的图像经过点![]() ,且与线段
,且与线段![]() 始终有交点(含端点),若
始终有交点(含端点),若![]() ,则
,则![]() 的值可能为( )
的值可能为( )
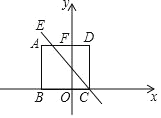
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com