
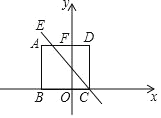
【题目】如图所示, 在平面直角坐标系中, 边长为![]() 的正方形
的正方形![]() 的边
的边![]() 在
在![]() 轴上,
轴上, ![]() 交
交![]() 轴于点
轴于点![]() ,一次函数
,一次函数![]() 的图像经过点
的图像经过点![]() ,且与线段
,且与线段![]() 始终有交点(含端点),若
始终有交点(含端点),若![]() ,则
,则![]() 的值可能为( )
的值可能为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
根据正方形的边长与BO=2CO,求得B、C两点坐标,再求得A、F的坐标,把C点坐标代入y=kx+b中,得b关于k的代数式,得到新解析式,然后把y=3代入新解析式,求得x关于k的代数式,再根据直线y=kx+b与线段AF始终有交点(含端点),由此时交点的横坐标的取值范围列出k的不等式组,便可求得k的取值范围,进而得解.
∵BC=3,BO=2CO,
∴OC=1,OB=2,
∴B(2,0),C(1,0),
∴A(2,3),F(0,3),
把C(1,0)代入y=kx+b(k≠0)中,得b=k,
∴一次函数为y=kxk,
当y=3时,kxk=3,
∴![]() ,
,
∴直线CE与AF的交点坐标为(![]() ,3)
,3)
∵一次函数y=kx+b的图像与线段AF始终有交点(含端点),
∴2![]() 0,
0,
由函数图像知,k<0,
∴2kk+30,
∴3k1,
故选:C.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】如图,半径为2的⊙O分别与x轴,y轴交于A,D两点,⊙O上两个动点B,C,使∠BAC=60°恒成立,设△ABC的重心为G,则DG的最小值是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为美化小区,物业公司计划对面积为![]() 的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队的
的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队的![]() 倍,如果要独立完成面积为
倍,如果要独立完成面积为![]() 区域的绿化,甲队比乙队少用
区域的绿化,甲队比乙队少用![]() 天.
天.
![]() 求甲、乙两工程队每天能完成绿化的面积分别是多少
求甲、乙两工程队每天能完成绿化的面积分别是多少![]() ?
?
![]() 若物业公司每天需付给甲队的绿化费用为
若物业公司每天需付给甲队的绿化费用为![]() 万元,需付给乙队的费用为
万元,需付给乙队的费用为![]() 万元,要使这次的绿化总费用不超过
万元,要使这次的绿化总费用不超过![]() 万元,至少应安排甲队工作多少天?
万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组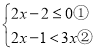
请结合题意填空,完成本题的解答
(1)解不等式①,得___________;
(2)解不等式②,得___________;
(3)把不等式①和②的解集在数轴上表示出来:
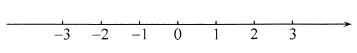
(4)原不等式组的解集为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() 均在格点上.
均在格点上.
(Ⅰ)![]() 的长等于________________;
的长等于________________;
(Ⅱ)在如图所示的网格中,将![]() 绕点A旋转,使得点B的对应点
绕点A旋转,使得点B的对应点![]() 落在边
落在边![]() 上,得到
上,得到![]() ,请用无刻度的直尺,画出
,请用无刻度的直尺,画出![]() ,并简要说明这个三角形的各个顶点是如何找到的(不要求证明).
,并简要说明这个三角形的各个顶点是如何找到的(不要求证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,
,![]()
(1) 将![]() 向右平移6个单位长度至
向右平移6个单位长度至![]() , 再将
, 再将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至
至![]() ,请按要求画出图形;
,请按要求画出图形;
(2)在![]() 的变换过程中,直接写出点
的变换过程中,直接写出点![]() 的运动路径长
的运动路径长
(3)![]() 可看成
可看成![]() 绕某点
绕某点![]() 旋转
旋转![]() 得到的, 则点
得到的, 则点![]() 的坐标为
的坐标为

查看答案和解析>>
科目:初中数学 来源: 题型:
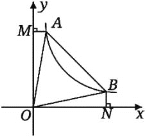
【题目】如图,直线![]() 与双曲线
与双曲线![]() 交于A、B两点,连接OA、OB,
交于A、B两点,连接OA、OB,![]() 轴于点M,
轴于点M,![]() 轴于点N,有以下结论:①
轴于点N,有以下结论:①![]() ;②
;②![]() ;③
;③![]() 则
则![]() ;④当
;④当![]() 时,
时,![]() .其中结论正确的是___________
.其中结论正确的是___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在小正方形的边长均为l的方格纸中,有线段AB,BC.点A,B,C均在小正方形的顶点上.
(1)在图1中画出四边形ABCD,四边形ABCD是轴对称图形,点D在小正方形的项点上:
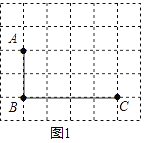
(2)在图2中画四边形ABCE,四边形ABCE不是轴对称图形,点E在小正方形的项点上,∠AEC=90°,EC>EA;直接写出四边形ABCE的面积为________.
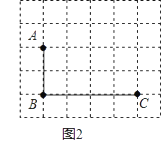
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】茶叶是安徽省主要经济作物之一,2020年新茶上市期间,某茶厂为获得最大利益,根据市场行情,把新茶价格定为400元/kg,并根据历年的相关数据整理出第x天(1≤x≤15,且x为整数)制茶成本(含采摘和加工)和制茶量的相关信息如下表.假定该茶厂每天制作和销售的新茶没有损失,且能在当天全部售出(当天收入=日销售额-日制茶成本)
制茶成本(元/kg) | 150+10x |
制茶量(kg) | 40+4x |
(1)求出该茶厂第10天的收入;
(2)设该茶厂第x天的收入为y(元).试求出y与x之间的函数关系式,并求出y的最大值及此时x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com