
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,
,![]()
(1) 将![]() 向右平移6个单位长度至
向右平移6个单位长度至![]() , 再将
, 再将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至
至![]() ,请按要求画出图形;
,请按要求画出图形;
(2)在![]() 的变换过程中,直接写出点
的变换过程中,直接写出点![]() 的运动路径长
的运动路径长
(3)![]() 可看成
可看成![]() 绕某点
绕某点![]() 旋转
旋转![]() 得到的, 则点
得到的, 则点![]() 的坐标为
的坐标为

【答案】(1)图见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用点平移的坐标规律得出点![]() 的坐标,然后描点、顺次连接即可得
的坐标,然后描点、顺次连接即可得![]() ;利用旋转的性质画出点
;利用旋转的性质画出点![]() ,再顺次连接即可得
,再顺次连接即可得![]() ;
;
(2)点C的运动路径长为平移的距离与弧![]() 的长之和,先求出
的长之和,先求出![]() 的长,再利用弧长公式计算即可得;
的长,再利用弧长公式计算即可得;
(3)作![]() 和
和![]() 的垂直平分线,它们的交点即为点P,点绕某点(非原点)旋转
的垂直平分线,它们的交点即为点P,点绕某点(非原点)旋转![]() 的坐标变换规律得出点
的坐标变换规律得出点![]() 的坐标,再设点P的坐标为
的坐标,再设点P的坐标为![]() ,根据点绕某点(非原点)旋转
,根据点绕某点(非原点)旋转![]() 的坐标变换规律可得一个关于a、b的二元一次方程组,求解即可得.
的坐标变换规律可得一个关于a、b的二元一次方程组,求解即可得.
(1)由点平移的坐标规律得:![]()
即![]()
描点、顺次连接得到![]() ,如图所示:
,如图所示:
由旋转的性质画出点![]() ,再顺次连接得到
,再顺次连接得到![]() ,如图所示:
,如图所示:
(2)由平移的性质得:![]()
![]()
![]()
![]() 弧
弧![]() 的长为
的长为![]()
则点![]() 的运动路径长为
的运动路径长为![]()
故答案为:![]() ;
;
(3)作![]() 和
和![]() 的垂直平分线,它们的交点即为点P,如图所示:
的垂直平分线,它们的交点即为点P,如图所示:
理由:由旋转的性质可知,![]()
由线段垂直平分线的性质得:点P既在![]() 的垂直平分线上,也在
的垂直平分线上,也在![]() 的垂直平分线上
的垂直平分线上
则它们的交点即为点P
点P的坐标求解过程如下:
由点绕某点(非原点)旋转![]() 的坐标变换规律得:
的坐标变换规律得:![]()
即![]()
设点P的坐标为![]()
则有![]()
解得![]()
故点P的坐标为![]()
故答案为:![]() .
.



科目:初中数学 来源: 题型:
【题目】在“前线医护人员”和全国人民的共同努力下,疫情得到了有效控制,宁波各大企业复工复产有序进行.为了实现员工“一站式”返岗,宁波某企业打算租赁5辆客车前往宁波东站接员工返岗.已知现有A、B两种客车,A型客车的载客量为45人/辆,每辆租金为400元;B型客车的载客量为30人/辆,每辆租金为280元.设租用A型客车为x辆,所需费用为y元.
(1)求y关于x的函数解析式;
(2)若该企业需要接的员工有205人,请求出租车费用最小值,并写出对应的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (
(![]() ,
,![]() ,
,![]() 是常数,
是常数,![]() )的自变量x与函数值y的部分对应值如下表:
)的自变量x与函数值y的部分对应值如下表:
| … | -1 | 0 | 1 | 3 | … |
| … |
| 3 |
| 3 | … |
且当![]() 时,与其对应的函数值
时,与其对应的函数值![]() .有下列结论:①
.有下列结论:①![]() ;②3是关于
;②3是关于![]() 的方程
的方程![]() 的一个根;③
的一个根;③![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示, 在平面直角坐标系中, 边长为![]() 的正方形
的正方形![]() 的边
的边![]() 在
在![]() 轴上,
轴上, ![]() 交
交![]() 轴于点
轴于点![]() ,一次函数
,一次函数![]() 的图像经过点
的图像经过点![]() ,且与线段
,且与线段![]() 始终有交点(含端点),若
始终有交点(含端点),若![]() ,则
,则![]() 的值可能为( )
的值可能为( )
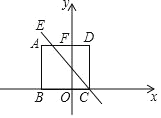
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y = ax2+ bx + c (a≠0)的图象如图所示,下列结论中:
①abc>0;②2a + b>0;③a +b<m(am +b)(m≠1);④(a+c)2< b2;⑤a >1.其中正确的项是( )
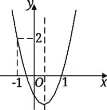
A.①②⑤B.①③④C.①②④D.②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于点A,B(1,0),与
与x轴交于点A,B(1,0),与![]() 轴交于点C(0,3),对称轴为直线
轴交于点C(0,3),对称轴为直线![]() .
.
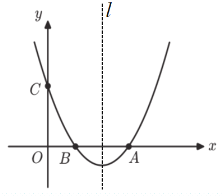
(1)求抛物线的解析式及点A的坐标;
(2)在对称轴![]() 上是否存在一点M,使得△BCM周长最小?若存在,求出△BCM周长;若不存在,请说明理由;
上是否存在一点M,使得△BCM周长最小?若存在,求出△BCM周长;若不存在,请说明理由;
(3)若点P是抛物线上一动点,从点C沿抛物线向点A运动,过点P作PD//![]() 轴,交AC于点D,当△ADP是直角三角形时,求点P的坐标.
轴,交AC于点D,当△ADP是直角三角形时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了帮助我市一名贫困学生,某校组织捐款,现从全校所有学生的捐款数额中随机抽取10名学生的捐款数统计如下表:
捐款金额/元 | 20 | 30 | 50 | 90 |
人数 | 2 | 4 | 3 | 1 |
则下列说法正确的是( )
A. 10名学生是总体的一个样本
B. 中位数是40
C. 众数是90
D. 方差是400
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)经过点A(1,-1)、B(3,3),且当1≤x≤3时,-1≤y≤3,则a的取值范围是___________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com