
【题目】如图,已知在菱形![]() 中,
中,![]() , 则菱形
, 则菱形![]() 的边长等于____________
的边长等于____________
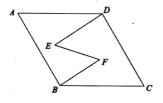
【答案】![]()
【解析】
作BG⊥EF,连接BD,与EF相交于点H,由三角函数求出BG和GF的长度,然后得到EG的长度,由DE∥BF,则△DEH∽△BFH,则![]() ,设GH=x,则EH=2+x,FH=3-x,代入求出GH,再由勾股定理求出BH,得到BD的长度,即可得到菱形的边长.
,设GH=x,则EH=2+x,FH=3-x,代入求出GH,再由勾股定理求出BH,得到BD的长度,即可得到菱形的边长.
解:作BG⊥EF,连接BD,与EF相交于点H,如图:
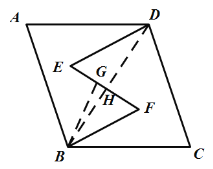
∵DE∥BF,
∴∠F=∠E,
∴sin∠F=sin∠E=![]() ,
,
∵BG⊥EF,
∴![]() ,
,
∵BF=EF=5,
∴BG=4,
∴FG=![]() ,
,
∴EG=5![]() ;
;
∵DE∥BF,
∴△DEH∽△BFH,
∴![]() ,
,
设GH=x,则EH=2+x,FH=3-x,
∴![]() ,
,
解得:![]() ,
,
∴![]() ;
;
在Rt△BGH中,由勾股定理,得
![]() ,
,
∴![]() ;
;
∵∠A=60°,AB=AD,
∴△ABD是等边三角形,
∴![]() ;
;
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a=4,b=5,则该矩形的面积为( )
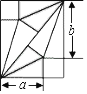
A.50B.40C.30D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AG⊥BC,垂足为点G,点E为边AC上一点,BE=CE,点D为边BC上一点,GD=GB,连接AD交BE于点F.
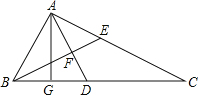
(1)求证:∠ABE=∠EAF;
(2)求证:AE2=EFEC;
(3)若CG=2AG,AD=2AF,BC=5,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是以BC为底的等腰三角形,AD是边BC上的高,点E、F分别是AB、AC的中点.
(1)求证:四边形AEDF是菱形;
(2)如果四边形AEDF的周长为12,两条对角线的和等于7,求四边形AEDF的面积S.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为美化小区,物业公司计划对面积为![]() 的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队的
的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队的![]() 倍,如果要独立完成面积为
倍,如果要独立完成面积为![]() 区域的绿化,甲队比乙队少用
区域的绿化,甲队比乙队少用![]() 天.
天.
![]() 求甲、乙两工程队每天能完成绿化的面积分别是多少
求甲、乙两工程队每天能完成绿化的面积分别是多少![]() ?
?
![]() 若物业公司每天需付给甲队的绿化费用为
若物业公司每天需付给甲队的绿化费用为![]() 万元,需付给乙队的费用为
万元,需付给乙队的费用为![]() 万元,要使这次的绿化总费用不超过
万元,要使这次的绿化总费用不超过![]() 万元,至少应安排甲队工作多少天?
万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P的距离.(参考数据:![]() ≈2.449,结果保留整数)
≈2.449,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组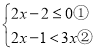
请结合题意填空,完成本题的解答
(1)解不等式①,得___________;
(2)解不等式②,得___________;
(3)把不等式①和②的解集在数轴上表示出来:
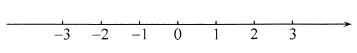
(4)原不等式组的解集为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,
,![]()
(1) 将![]() 向右平移6个单位长度至
向右平移6个单位长度至![]() , 再将
, 再将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至
至![]() ,请按要求画出图形;
,请按要求画出图形;
(2)在![]() 的变换过程中,直接写出点
的变换过程中,直接写出点![]() 的运动路径长
的运动路径长
(3)![]() 可看成
可看成![]() 绕某点
绕某点![]() 旋转
旋转![]() 得到的, 则点
得到的, 则点![]() 的坐标为
的坐标为

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市特产大闸蟹,2016年的销售额是![]() 亿元,因生态优质美誉度高,销售额逐年增加2018年的销售额达
亿元,因生态优质美誉度高,销售额逐年增加2018年的销售额达![]() 亿元,若2017、2018年每年销售额增加的百分率都相同.
亿元,若2017、2018年每年销售额增加的百分率都相同.
(1)求平均每年销售额增加的百分率;
(2)该市这![]() 年大闸蟹的总销售额是多少亿元?
年大闸蟹的总销售额是多少亿元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com