
【题目】已知:二次函数y = ax2+ bx + c (a≠0)的图象如图所示,下列结论中:
①abc>0;②2a + b>0;③a +b<m(am +b)(m≠1);④(a+c)2< b2;⑤a >1.其中正确的项是( )
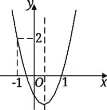
A.①②⑤B.①③④C.①②④D.②④⑤
【答案】A
【解析】
由抛物线的开口方向判断a的符号,由抛物线与y轴的交点判断c的符号,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解:①∵抛物线的开口向上,∴a>0,
∵与y轴的交点为在y轴的负半轴上,∴c<0,
∵对称轴为x=-![]() >0,
>0,
∴a、b异号,即b<0,
又∵c<0,∴abc>0,
故结论①正确;
②∵对称轴为x=-![]() <1,a>0,
<1,a>0,
∴-b<2a,
∴2a+b>0;
故结论②正确;
③当x=1时,y1=a+b+c;
当x=m时,y2=m(am+b)+c,当m>1,y2>y1;当m<1,y2<y1,所以不能确定;
故结论③错误;
④当x=1时,a+b+c=0;
当x=-1时,a-b+c>0;
∴(a+b+c)(a-b+c)=0,即(a+c)2-b2=0,
∴(a+c)2=b2
故结论④错误;
⑤当x=-1时,a-b+c=2;
当x=1时,a+b+c=0,
∴a+c=1,
∴a=1+(-c)>1,即a>1;
故结论⑤正确;
综上所述,正确的是①②⑤.
故选:A.


科目:初中数学 来源: 题型:
【题目】为了解我市某中学“书香校园”的建设情况,在该校随机抽取了50名学生,调查了解他们一周阅读课外书籍的时间,并将调查结果绘制成如图所示的频数分布直方图(每小组的时间包含最小值,不包含最大值),根据图中信息估计该校1500名学生中,一周课外阅读时间不少于4小时的人数约为( )
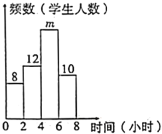
A.300B.600C.900D.1200
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P的距离.(参考数据:![]() ≈2.449,结果保留整数)
≈2.449,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个矩形纸片![]() 放置在平面直角坐标系中,点
放置在平面直角坐标系中,点![]() ,点
,点![]() ,点E,F分别在边
,点E,F分别在边![]() ,
,![]() 上.沿着
上.沿着![]() 折叠该纸片,使得点A落在
折叠该纸片,使得点A落在![]() 边上,对应点为
边上,对应点为![]() ,如图①.再沿
,如图①.再沿![]() 折叠,这时点E恰好与点C重合,如图②.
折叠,这时点E恰好与点C重合,如图②.
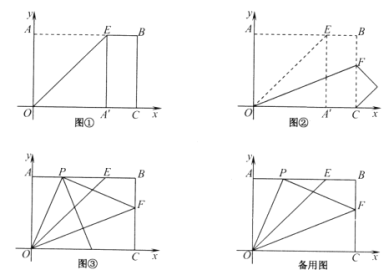
(Ⅰ)求点C的坐标;
(Ⅱ)将该矩形纸片展开,再折叠该矩形纸片,使点O与点F重合,折痕与![]() 相交于点P,展开矩形纸片,如图③.
相交于点P,展开矩形纸片,如图③.
①求![]() 的大小;
的大小;
②点M,N分别为![]() ,
,![]() 上的动点,当
上的动点,当![]() 取得最小值时,求点N的坐标(直接写出结果即可).
取得最小值时,求点N的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,
,![]()
(1) 将![]() 向右平移6个单位长度至
向右平移6个单位长度至![]() , 再将
, 再将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至
至![]() ,请按要求画出图形;
,请按要求画出图形;
(2)在![]() 的变换过程中,直接写出点
的变换过程中,直接写出点![]() 的运动路径长
的运动路径长
(3)![]() 可看成
可看成![]() 绕某点
绕某点![]() 旋转
旋转![]() 得到的, 则点
得到的, 则点![]() 的坐标为
的坐标为

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,在A,B两地之间有汽车站C站,货车由A地驶往B地,客车由B地驶往C站.两车同时出发,匀速行驶.图2是货车、客车离C站的路程y1,y2(千米)与行驶时间x(小时)之间的函数关系图象.
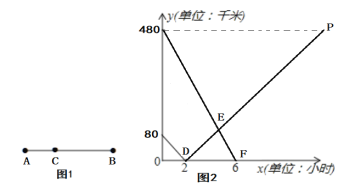
(1)填空:A,B两地相距 千米;
(2)求两小时后,货车离C站的路程y1与行驶时间x之间的函数关系式;
(3)客、货两车何时相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
(1)求证:直线PB与⊙O相切;
(2)PO的延长线与⊙O交于点E.若⊙O的半径为3,PC=4.求弦CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年春节前夕,一场突如其来的新冠肺炎疫情牵动着全国人民的心,因疫情发展迅速,全国口罩等防护用品成了年货,供应紧张.某药店用2000元购进某品牌的一批口罩后,供不应求,又用5000元购进这种口罩,第二批口罩的数量是第一批的2倍,但进货单价比第一批贵2元.
(1)第一批口罩进货单价多少元?
(2)若两次购进口罩按同一价格销售,两批全部售完后,获利不少于2000元,那么销售单价至少为多少元?
(3)由于党的好政策,爱心工人加班加点地生产,口罩变得不再紧俏,药店第三批进货单价比第一批便宜1元,若按照(2)中销售单价出售,每天可以售出60个,药店为了促销,决定降低一定的价格,每降低一元,每天多售出20个,问单价定为多少时,每天利润最大?最大是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】茶叶是安徽省主要经济作物之一,2020年新茶上市期间,某茶厂为获得最大利益,根据市场行情,把新茶价格定为400元/kg,并根据历年的相关数据整理出第x天(1≤x≤15,且x为整数)制茶成本(含采摘和加工)和制茶量的相关信息如下表.假定该茶厂每天制作和销售的新茶没有损失,且能在当天全部售出(当天收入=日销售额-日制茶成本)
制茶成本(元/kg) | 150+10x |
制茶量(kg) | 40+4x |
(1)求出该茶厂第10天的收入;
(2)设该茶厂第x天的收入为y(元).试求出y与x之间的函数关系式,并求出y的最大值及此时x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com