
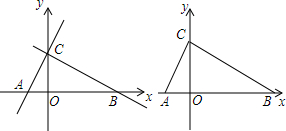
���� �ٸ���ֱ�������ε��������A��C�����꣬Ȼ�����ô���ϵ������⣻
�ڷֳ�P���߶�AC�Ϻ���AC���ӳ�������������������ۣ����P��Q�����꣬��d��������t��ʾ��
�۸��ݢڵĽ���Լ�PA=$\frac{5}{6}$d�������t��ֵ��Ȼ��֤����EMO�ա�BCP�����ɽ��
��� �⣺�١�ֱ�ǡ�ABC�У���ACB=90�㣬��BAC=60�㣬
���ABC=30�㣬
��AC=$\frac{1}{2}$AB=$\frac{1}{2}$��8=4��
�֡�ֱ�ǡ�AOC�У���ACO=30�㣬
��OA=$\frac{1}{2}$AC=$\frac{1}{2}$��4=2��
��OC=$\sqrt{A{C}^{2}-O{A}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$��
��A�������ǣ�-2��0����C�������ǣ�0��2$\sqrt{3}$����
��AC�Ľ���ʽ��y=kx+b��
��$\left\{\begin{array}{l}{-2k+b=0}\\{b=2\sqrt{3}}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=\sqrt{3}}\\{b=2\sqrt{3}}\end{array}\right.$��
��ֱ��AC�Ľ���ʽ��y=$\sqrt{3}$x+2$\sqrt{3}$��
��OB=AB-OA=8-2=6����B�������ǣ�6��0����
��BC�Ľ���ʽ��y=mx+n��
��$\left\{\begin{array}{l}{-6m+n=0}\\{n=2\sqrt{3}}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{m=-\frac{\sqrt{3}}{3}}\\{n=2\sqrt{3}}\end{array}\right.$��
��BC�Ľ���ʽ��y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$��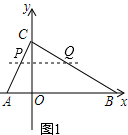 ��-2��t��0ʱ����ͼ1��
��-2��t��0ʱ����ͼ1��
��x=t����y=$\sqrt{3}$x+2$\sqrt{3}$�ã�
y=$\sqrt{3}$t+2$\sqrt{3}$��
��P�������ǣ�t��$\sqrt{3}$t+2$\sqrt{3}$����
��y=$\sqrt{3}$t+2$\sqrt{3}$����y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$��
�ã�$\sqrt{3}$t+2$\sqrt{3}$=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$��
��ã�x=-3t��
��Q�������ǣ�-3t��$\sqrt{3}$t+2$\sqrt{3}$����
��d=-3t-t=-4t��
��t��0ʱ����ͼ2��ͬ�����P�������ǣ�t��$\sqrt{3}$t+2$\sqrt{3}$����
Q�������ǣ�-3t��$\sqrt{3}$t+2$\sqrt{3}$����
��d=t-��-3t��=4t��
�۵�-2��t��0ʱ��PA=2��t+2������2��t+2��=$\frac{5}{6}$��-4t�������t=-$\frac{1}{4}$��
OE��OB��BC��BP����������������P���߶�AC���ӳ����ϣ��ɢڿɵ�AP=4+2t����PA=$\frac{5}{6}$d��4+2t=$\frac{5}{6}$��4t��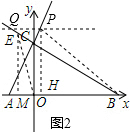
��ã�t=3��
��APB=30��+��OEB��
�����ǣ�BH=3��DH=5$\sqrt{3}$��PB2=9+75=84��
AP=10��PC=6��BC=4$\sqrt{3}$��
��EM=$\sqrt{3}$x��BM=3x����$\sqrt{3}$x��2+��3x-6��2=84����ã�x=4��
��EM=4$\sqrt{3}$��OM=12-6=6��
�ڡ�EMO�͡�BCP�У�
$\left\{\begin{array}{l}{EM=BC}\\{��EMO=��PCB}\\{OM=PC}\end{array}\right.$��
���EMO�ա�BCP��
���MOE=��CPB=��OBE+��OEB��
���APB=30��+��OEB��
���� ���⿼���˴���ϵ������������ʽ�Լ�ȫ�������ε��ж������ʣ���ȷ֤����EMO�ա�BCP�ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �������ϱ�ʾa��b��0�������λ����ͼ��ʾ����$\sqrt{��a+b��^{2}}$-|a-b|��
�������ϱ�ʾa��b��0�������λ����ͼ��ʾ����$\sqrt{��a+b��^{2}}$-|a-b|���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
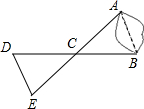 ��ͼ��A��B����ֱ�λ��һ�����������࣬����������һ��ˮ��D����BD���е�C����һ�ð��������С����A��������ֱ��ACһֱ��ǰ������C�ߵ���E��A��C��E������ͬһ��ֱ���ϣ�����ʹCE=CA��Ȼ����������E��ˮ��D�ľ��룬��DE�ij��Ⱦ���A��B����֮��ľ��룮
��ͼ��A��B����ֱ�λ��һ�����������࣬����������һ��ˮ��D����BD���е�C����һ�ð��������С����A��������ֱ��ACһֱ��ǰ������C�ߵ���E��A��C��E������ͬһ��ֱ���ϣ�����ʹCE=CA��Ȼ����������E��ˮ��D�ľ��룬��DE�ij��Ⱦ���A��B����֮��ľ��룮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
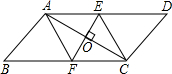 ��?ABCD�У��Խ���AC�Ĵ�ֱƽ���߷ֱ���AD��BC�ཻ�ڵ�E��F����AC���ڵ�O����֤���ı���AECF�����Σ�
��?ABCD�У��Խ���AC�Ĵ�ֱƽ���߷ֱ���AD��BC�ཻ�ڵ�E��F����AC���ڵ�O����֤���ı���AECF�����Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
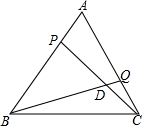 ��ͼ����ABC�ǵȱ������Σ�AB=2cm������P��Q�ֱ�ӵ�A��Cͬʱ�������˶��ٶȾ�Ϊ1cm/s����P�ӵ�A��������A��B�˶�������Bֹͣ����Q�ӵ�C��������C��A�˶�������Aֹͣ������BQ��CP�ཻ�ڵ�D�����P���˶�ʱ��Ϊx��s����
��ͼ����ABC�ǵȱ������Σ�AB=2cm������P��Q�ֱ�ӵ�A��Cͬʱ�������˶��ٶȾ�Ϊ1cm/s����P�ӵ�A��������A��B�˶�������Bֹͣ����Q�ӵ�C��������C��A�˶�������Aֹͣ������BQ��CP�ཻ�ڵ�D�����P���˶�ʱ��Ϊx��s�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
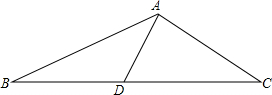 ��ͼ���ڡ�ABC�У�AC=4cm��BC=10cm��BC���ϵ�����AD=3cm�����ABD�������
��ͼ���ڡ�ABC�У�AC=4cm��BC=10cm��BC���ϵ�����AD=3cm�����ABD��������鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com